Кружкология
Кружкология — наука, изучающая кружки.
Исторический экскурс[править]
Как таковая кружкология зародилась в Бронзовом веке. По дошедшим до нашего времени многочисленным свидетельствам очевидцев, была свидетелем бурного расцвета и заката Бронтозавров (бронированных динозавров). В средние века внезапно получила альтернативное направление, официально именуемое в разного рода энциклопедиях как «Церковная кружка» или «Кружка из циркония». В эру научно-технической революции неким Эсмархом была адаптирована для устранения разного рода непроходимости в человеческих индивидуумах при помощи сложной системы резинотехнических изделий, получившей название по автору «Кружка Эсмарха».
Краткое описание[править]
Кружкология — очень сложная наука. Например: ровный круг — क़ॗॎऄॏ॓0098977890ऋिश, угловатый круг — तणुल009778ॕॿद0098॓009335॔.
В кружкологии используется алфавит девангари. Но также используются кхмерские буквы и канадское слоговое письмо. Например слово «кружкология» записывают: ᘳᖽᘒᕮᗝᒠᗝᕮ (круголог).
Ввиду сугубой сложности кружкологии учёные кружкологи периодически впадают в депрессию:
В этом случае, кружкологов возводят в квадрат (процесс, известный под названием «квадратура круга») или вписывают в Куб, где оставляют до полной реабилитации.
Ниже рассказано об основных проблемах кружкологии.
Проблема классификации[править]
Кружкологи делают многочисленные попытки провести полную классификацию известных науке кружков. Были выявлены многочисленные характеристики кружков, такие как пол, цвет, форма, объём, материал, локация, возраст, социальная принадлежность и др. И здесь открылась Основная проблема кружкологии: ни одну из найденных характеристик невозможно применить ко всем известным кружкам. Таким образом, непонятно, как кружки классифицировать.
Правило Буравчика[править]
Выдающийся учёный Иоганн Буравчик высказал гипотезу, которая подтверждается всеми исследованиями, однако до сих пор не доказана:
|
Не существует кружка, к которому были бы применимы все известные характеристики кружков одновременно. |
Эта гипотеза получила название Правило Буравчика.
Исследователи научного наследия Буравчика нашли среди его рукописей следующие пометки: «Это противоречит самой сути кружков» и «Я нашёл этому поистине чудесное доказательство, но поля книги слишком узки для него».
Простота формулировки правила Буравчика, доступная в понимании даже школьнику, и отстуствие доказательства, вдохновляют многих на попытки найти это доказательство. Сообщество кружкологов Великобритании установило специальную премию за нахождение оного, однако это не помогло: доказательство до сих пор не найдено.
Однако эмпирические данные подтверждают правоту Буравчика.
Примеры частично классифицированных кружков[править]
Ниже приведены примеры некоторых хорошо исследованных кружков и их характеристик.
Пивная кружка. Женская. Цвет и материал варьируются. Локация варьируется. По объёму пивные кружки подразделются пинтовые, полу-пинтовые и двухпинтовые. Обычным наполнением считаются воздух, пиво, пена, или сочетание вышеперечисленного; однако иногда наблюдаются другие варианты: квас, бурда, денежные купюры, окурки, мелкие бытовые предметы и малоисследованная жидкость под названием «что за отрава».
Детская кружка. Женская, пёстрая, пластиковая. Хорошо поддаётся измерению объёма. Наполнение варьируется. Локация варьируется.
Кружок мягкой игрушки. Мужской, пёстрый, мягкий, неправильный. К.м.и. не является правильным кругом по форме, так как имеет многочисленные выросты, выходящие за рамки граничной окружности. Локация варьируется; наблюдения показывают, что наиболее частыми локациями к.м.и. являются дома детского творчества, школы и клубы программы «Долголетие». Также выдвинута гипотеза о возможности установления содержимого этого кружка, однако для этого требуется частично повредить его поверхность. Доказана возможность установить объём к.м.и. и выдвинута любопытная гипотеза о частичной зависимости объёма к.м.и. от степени его наполненности. Это делает к.м.и. одним из наиболее поддающихся классифицированию.
Венский кружок. Мужской. Предположительно неправильный (см. изображение). Локация — Вена. Такие характеристики как материал, объём и цвет к этому кружку неприменимы. Наблюдения показывают, что это очень позитивистский кружок. Также является единственным известным науке кружком, к которому применима характеристика «логический». Таким образом, в.к. является одним из наиболее уникальных известных кружков.
Рабочий кружок. Мужской. Формальная локация — Нью-Йорк; однако наблюдается также в других городах, напр. Бостон, Торонто, Амхерст, а также в печати и в интернете. Понятия формы, цвета, материала и объёма неприменимы. Вопреки названию, принадлежность р.к. к социальному классу «рабочие» опровергнута наблюдениями, так как в р.к. замечена очень большая доля трудовой интеллигенции. Языковая принадлежность — идиш, однако наблюдаются также русский, английский, французский и иврит. В общем, что это за кружок такой, учёным ещё предстоит выяснить.
(ИЗОБРАЖЕНИЕ ОСУТСТВУЕТ) Подпольный рабочий кружок (не путать с «рабочим кружком»). Мужской. Предположительно рабочий. Локация — глубокое подполье. Подполье предположительно находилось в Петрограде и других крупных городах Российской империи. Это, собственно всё, что о нём известно, так как кружок прекратил существование в 1917 году и исследовать его попросту некому.
Круги Архимеда. Пол не установлен. Плоские, вследствие чего понятие объёма и наполнения неприменимы. Локация — Сиракузы, Греция. Учёные до сих пор не могут объяснить, для чего Архимед нарисовал три серых, два белых и голубой круги, а также два лиловых овала. Таинственная надпись «3:2» представляется началом объяснения и порождает много нездоровых фантазий, полностью развенчанных математиками. По-видимому, Архимед сделал открытие, достойное возгласа «Эврика!», но описание открытия утрачено. В день, когда Архимед совершил своё открытие, жители Сиракуз были пьяны и невосприимчивы к научным лекциям, а ворвавшиеся в Сиракузы римские воины заподозрили в кругах то ли шпионскую провокацию, то ли дискредитацию войск Священной Римской империи и казнили Архимеда без суда и следствия. Отсюда вытекает мораль: сначала любыми средствами выпытай у учёного смысл его выкладок, а уже потом — казни.
Свой круг. Один из немногих кружков, к которому применима характеристика свой-чужой. Никакие другие характеристики к этому кружку пока применить не удалось. Известна множественная вариация этого кружка — круги своя, однако эти круги ещё хуже поддаются классификации, чем одиночный с.к.
Кружка Эсмарха. Женская, резиновая, красная. Хорошо поддаётся измерению объёма. Наполнение варьируется. Локация варьируется. Единственная известная улыбающаяся кружка (см. рисунок). Предположительно злая, хотя некоторые исследователи сообщают, что после общения с этой кружкой испытывают большое облегчение. Однако все сходятся на том, что исследование к.э. вызывает неодолимое желание пробежаться с максимально возможной для исследователя скоростью.
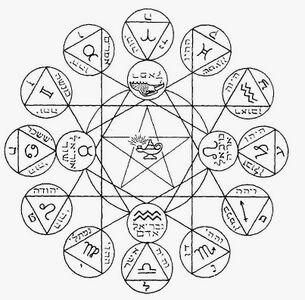
Кольцо пятерых, известное также как квинтовый круг.
Самый загадочный кружок. Понятия пола, локации, материала, объёма, цвета и социальной принадлежности неприменимы.
Однако применимы такие характеристики как цикличность, равный темперамент (англ. equal temperament)[Ааа, что это?] и высота тона.
В этом кружке замечены великолепные пятёрки [А это ещё что?]. Также некоторые части к.п. отмечены как острые (англ. sharp) и некоторые как плоские (англ. flat).
Британские учёные также обнаружили в к.п. пифагорейскую запятую (англ. Pythagorean comma) и системы риального тюнинга.
О кольце пятерых написаны толстенные тома исследований, начатых ещё Пифагором, однако каждое новое исследование порождает новые вопросы, и конца им не предвидится.
Трудности изучения[править]
Учёным кружкологам приходится нелегко. Но ещё труднее приходится будущим кружкологам — студентам, изучающим кружкологию в университетах. Не одна студенческая голова была сломана в процессе попытки получить диплом кружколога и приступить к профессиональному научному изучению кружков.
Ниже приведены примеры задач, которые приходится решать студентам-кружкологам.
Задача для начинающих[править]
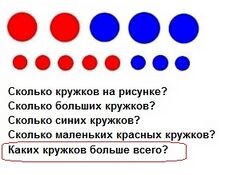
На рисунке 1 (справа) приведена задача, с которой сталкиваются студенты-кружкологи уже в первую неделю обучения. Задача касается определения характеристик кружков и распределения их по этим характеристикам, а также установления примерного количества кружков. Возможно, вам кажется, что это лёгкая задача. Тогда попробуйте ответить на последний вопрос.
Понятно, что маленьких кружков больше, чем больших, красных кружков больше, чем синих. Маленьких красных кружков больше, чем маленьких синих, однако всех синих кружков больше, чем маленьких красных. Кружков, не являющихся маленькими и красными одновременно, граздо больше, чем маленьких красных. Но каких же кружков больше всего?
Правильный ответ вас удивит: больше всего всех кружков вместе!
Задача на подсчёт кружков[править]
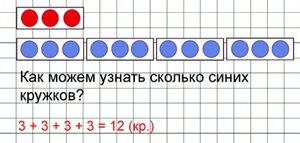
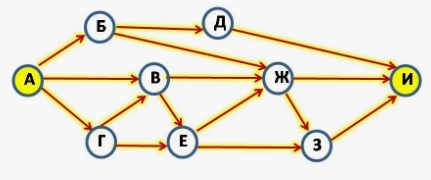
На рисунке 2 приведена типичная задача на подсчёт количества кружков.
Казалось бы, проще всего потыкать указкой в каждый и подсчитать: один, два, три, четыре… двенадцать. Однако правильным способом является объединение кружков в тройки, отсеивание тройки кружков, не подходящих по цвету, и подсчёт подходящих по цвету троек.
Почему к тройкам кружков не применятеся операция умножения, объясняется в учебнике статистической кружкологии, однако это объяснение занимает 2,5 страницы и отсылает к изложенным ранее теоремам, поэтому здесь мы его не приводим.
Задача на определение наполнения кружков[править]
На рисунке 3 (справа) — типичная задача на определение наполнения кружков.
Правильный ответ: не имеет значения, что и во что наливали, так как сосуды уже опустошены и начисто вымыты, что подтверждается простым визуальным наблюдением.
Из этой задачи выводится правило: важно не только правильно налить, но и вовремя выпить!
Гуманитарная кружкология[править]
Казалось бы, мало студентам сложнейших научных задач, их ещё заставляют рисовать, петь, танцевать и сочинять стихи. В итоге у лишённых дара стихосложения студентов получается нечто вроде следующего:
|
И это ещё только начало…
Трудность возрастает[править]
Ниже приведено ещё несколько типичных задач из задачников для студентов-кружкологов. Непосвящённому человеку трудно даже предположить, о чём идёт речь в этих задачах, а представьте, каково приходится студентам!
- Типичные задачи для студентов-кружкологов
Однако с настоящими трудностями кружколог столкнётся, когда закончит вуз и приступит к профессиональному исследованию такой загадочной сущности, как кружки. Впрочем, тот, кто смог получить диплом кружколога, уже готов ко всему.