Обсуждение:Самая лёгкая шахматная задача

Пояснение
	Друзья, вы, наверное, не поняли! Смысл этой статьи в том, что ЛЮБОЙ возможный ход за белых ведёт к мату. Так-то!
	Капитан Очевидность

Рис. 1

Рис. 2. Мат в 1, 2 или 3 хода

Рис. 3

Рис. 4

Девять вариантов это, конечно, круто. Поставьте белого коня на h5 и будет вам десятый вариант для круглого счастья. — 3 (обсуждение) 05:53, 10 марта 2019 (UTC)

Но ведь этим же самым конём мат можно и НЕ поставить, что значительно усложняет решение. Тот Самый Профессор (обсуждение) 12:17, 10 марта 2019 (UTC)

Ой, и правда. Я об этом не подумал, что можно пойти НЕ туда. — 3 (обсуждение) 16:49, 11 марта 2019 (UTC)

Только для белых

Эта задача самая простая только для белых, а для чёрных она слишком сложна. — Edward Chernenko^? 14:07, 10 марта 2019 (UTC)

Для чёрных это задача на обратный мат. Действительно, при ходе чёрных она слишком сложна: существует лишь 5 решений, тогда как аж 21 ход не ведёт к цели. Зато при ходе белых задача сводится к СЛШЗ. Тот Самый Профессор (обсуждение) 15:01, 11 марта 2019 (UTC)

Возможна ещё такая задача: продержаться за чёрных максимум ходов (то бишь 8): [1] Тот Самый Профессор (обсуждение) 15:20, 11 марта 2019 (UTC)

Запрос

Профессор, а не хотите ли модифицировать эту позицию так, чтобы у белых все-таки был единственный нематующий ход? Тогда позиция приобретёт истинную законченность, и откроется всем нам мудрость и нирвана.Ясен Перец (обсуждение) 07:33, 11 марта 2019 (UTC)

Это будет слишком сложно для начинающих. На этом этапе задача преподавателя — объяснить учащимся, кому именно нужно поставить мат --Луна Цедрейтер (обсуждение) 10:29, 11 марта 2019 (UTC)

А мы не ищем лёгких путей. Надо попутно объяснить учащимся, что иногда всё-таки мат в один ход не ставится. А то ведь учащиеся оборзеют вконец и будут двигать короля с а2 на с8 с радостным воплем «Мат!!!» Ясен Перец (обсуждение) 13:43, 11 марта 2019 (UTC)

Ясен Перец прав. Нефиг забивать начинающим шахматистам голову многовариантностью и обилием фигур на доске. Одного варианта достаточно. — 3 (обсуждение) 16:55, 11 марта 2019 (UTC)

Да хотя бы убрать с доски пешку f6. И опаньки! Есть нематующий ход, хотя и очень уж очевидный. Ясен Перец (обсуждение) 10:39, 12 марта 2019 (UTC)

А как насчёт задачи, где белые ставят мат любым ходом, кроме одного, и в случае этого хода чёрные любым своим ходом немедленно ставят мат? José Monteiro _discussão 15:08, 12 марта 2019 (UTC)

Я вынес этот вопрос на один из форумов... так вот: некий форумчанин (монстр в шахматах) ухитрился сотворить позицию всего лишь из семи фигур, полностью удовлетворяющую этим условиям. Как я его ни умолял открыть мне тайну сего золотого ключика, он лишь мерзко улыбался и предлагал мне поискать эту позицию самостоятельно. Но у меня нет ни малейших сомнений в том, что он-таки не врет. Ясен Перец (обсуждение) 06:08, 14 марта 2019 (UTC)

А тут, наверно, проще всего создать позицию, в которой у белых есть всего два хода, один из которых матует, а второй - нет. А на второй ход у черных есть один-единственный ход, который матует. И все ваши условия соблюдены. Ясен Перец (обсуждение) 17:20, 12 марта 2019 (UTC)

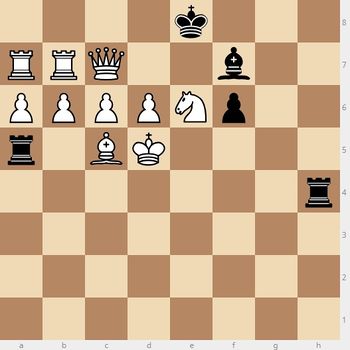
Вот пример такой позиции (рис. 3, если только я нигде не ошибся). У белых два матующих хода и один нематующий. В ответ на нематующий ход черные вынуждены поставить белым мат. Ясен Перец (обсуждение) 12:42, 13 марта 2019 (UTC)

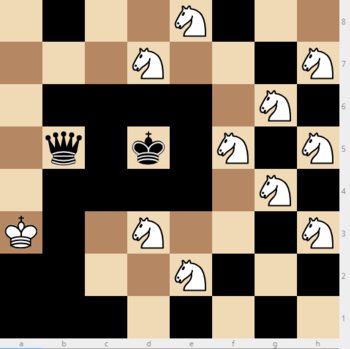
Или вот пример позиции на рис. 4. José Monteiro _discussão 20:18, 13 марта 2019 (UTC)

Да тут 4 хода не матуют. Тот Самый Профессор (обсуждение) 20:21, 13 марта 2019 (UTC)

Пофиксил позицию. José Monteiro _discussão 20:33, 13 марта 2019 (UTC)

Во-первых, файл обновится фиг знает когда, если вообще обновится (проще загрузить новый), во-вторых, теперь 3 хода не матуют. Тот Самый Профессор (обсуждение) 20:38, 13 марта 2019 (UTC)

Грузить новый необязательно, можно просто обновить страницу (Shift+F5 в Chrome, Shift+клик на кнопку Обновить в Firefox). Это сбрасывает кэш для всех (не только для обновившего страницу). — Edward Chernenko^? 20:48, 13 марта 2019 (UTC)

Но вообще идея с выколотыми полями хорошая. При достаточном числе таких полей на доске конь (единственная прыгающая фигура) будет определённо сильнее ферзя. Тот Самый Профессор (обсуждение) 20:44, 13 марта 2019 (UTC)

А как насчёт задачи, где белые ставят мат любым ходом, кроме одного, и в случае этого хода чёрные ставят мат любым ходом, кроме одного, и в случае этого хода белые ставят мат любым ходом, кроме одного, и в случае этого хода чёрные ставят мат любым ходом, кроме одного, и так до бесконечности? Тот Самый Профессор (обсуждение) 15:17, 12 марта 2019 (UTC)

Проще всего создать симметричную позицию, где оба короля могут ходить туда-сюда, а все остальные ходы матуют. Тот Самый Профессор (обсуждение) 15:25, 12 марта 2019 (UTC)

Это рано или поздно приведёт к троекратному повторению позиции. José Monteiro _discussão 17:39, 12 марта 2019 (UTC)

Да число возможных позиций вообще конечно, строго говоря. Тот Самый Профессор (обсуждение) 18:01, 12 марта 2019 (UTC)

Слишком сложно

Рис. 5

Я вот о чём подумал... А каков критерий «лёгкости» задачи? Можно, конечно, наплести невообразимое множество композиций, одна изощрённее другой, но облегчат ли они шахматную задачу до такого уровня, что она станет легче шашек? Наиболее лёгкой задачей является та, которая потребует от игрока наименьших затрат ресурсов — интеллектуальных и временны́х. Cледует предположить, что наиболее лёгкой шахматной задачей будет та, в которой соблюдены следующие

Условия мата

1. наименьшее количество фигур на доске, и
2. наименьшее количество возможных ходов, и
3. ход белых, и
4. мат ставится за один ход... без вариантов и шансов на ошибку.

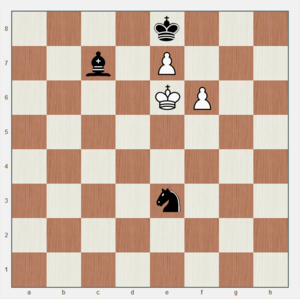
Исходя из этого, более элегантной композицией была бы та, в которой, чтобы поставить мат, белые могут сделать только один ход и только одной фигурой, а все остальные ходы недопустимы (например, так — рис. 5). — 3 (обсуждение) 22:35, 13 марта 2019 (UTC)

Если уж на то пошло, то самой легкой задачей будет позиция, в которой на доске готовый пат, а задание - белые начинают и делают ничью. Ясен Перец (обсуждение) 05:50, 14 марта 2019 (UTC)

Делать ничью — это уже задача для гроссмейстеров вроде Раклсена и Ракуаны. Тот Самый Профессор (обсуждение) 15:08, 14 марта 2019 (UTC)

Пат в один ход — идея очень заманчивая для самой легкой задачи, но я подозреваю, что для её реализации потребуется гораздо больше фигур, чем для мата. Соответственно, она проиграет в оптимальности мату. — 3 (обсуждение) 18:14, 14 марта 2019 (UTC)

Тут не требуется большого количества фигур. Белые Крh8, пешки d5, f7, g6, h7. Черные Крf8, пg7. Единственный ход белых d5-d6 пат. Хотя согласен, это действительно проигрывает мату если не в оптимальности, то в красоте. Ясен Перец (обсуждение) 14:10, 17 марта 2019 (UTC)

А как это — короли на соседних клетках? José Monteiro _discussão 14:16, 17 марта 2019 (UTC)

Я опечатался. Черный король на f8. Уже поправил.Ясен Перец (обсуждение) 14:20, 17 марта 2019 (UTC)

Поз. 6

Можно ещё меньше фигур (см. поз. 6). José Monteiro _discussão 14:37, 17 марта 2019 (UTC)

Тут нет пата после хода белых. У черных есть ход Кр:f7, и только теперь пат. Ясен Перец (обсуждение) 14:45, 17 марта 2019 (UTC)

А, да, я недоосмыслил условие. José Monteiro _discussão 14:53, 17 марта 2019 (UTC)

Белую пешку на f7 перекрасить не пробовал? Тот Самый Профессор (обсуждение) 16:34, 17 марта 2019 (UTC)

Тогда есть 1. ... Kpe8. José Monteiro _discussão 16:37, 17 марта 2019 (UTC)

Бля, ну я только откатить хотел, нельзя так быстро отвечать. Тот Самый Профессор (обсуждение) 16:39, 17 марта 2019 (UTC)

Тю, а зачем делать взаимный пат, когда пат чёрным можно объявить одной крайней пешкой? Тот Самый Профессор (обсуждение) 16:42, 17 марта 2019 (UTC)

У меня этот трюк не получился. То есть, это возможно, но тогда первый ход белых не будет единственным. А это одно из условий. Ясен Перец (обсуждение) 17:19, 17 марта 2019 (UTC)

Поз. 7

Поз. 8

Позиция 7. У белых есть единственный ход 1. Кр:d2. Пат. José Monteiro _discussão 16:48, 17 марта 2019 (UTC)

Ну если на доске 4х4, то да. :-)) А на доске 8х8 мне не удалось обойтись менее чем 7-ю фигурами. Ясен Перец (обсуждение) 17:13, 17 марта 2019 (UTC)

Если на доске 8x8 отказаться от использования только пешек, то можно обойтись меньшим числом фигур, например, как на позиции 8. José Monteiro _discussão 09:57, 18 марта 2019 (UTC)

Браво!!! Я как-то вообще не подумал о том, что белый король может быть под шахом. А теперь - вместо ферзя ставим черную пешку и добавляем белую пешку на g5. Итого 5 фигур и одни пешки. И еще можно ввести ограничение, что ход белых должен быть без взятия. Можно ли в этом случае обойтись менее чем 7-ю фигурами? Ясен Перец (обсуждение) 10:49, 18 марта 2019 (UTC)

Можно. Черного ферзя в поз. 8 убираем, и добавляем на доску одну черную пешку на g7 и две белые пешки на g6 и g5. Итого, шесть фигур -- короли и пешки, -- у белых возможен только один ход, этот ход без взятия, и он ведет к пату. — 3 (обсуждение) 17:04, 18 марта 2019 (UTC).

Интересно. Правда, в реальной игре эта позиция невозможна: чёрная пешка и раньше была на g7, тогда белый король не мог пойти на h6 — в шах. А как быть с реалистичными позициями? José Monteiro _discussão 17:09, 18 марта 2019 (UTC)

Совершенно верно, в реальной партии такая композиция невозможна. Но такого условия не было, чтобы позиция была реалистичной. Давайте его добавим. — 3 (обсуждение) 17:35, 18 марта 2019 (UTC)

Условия пата

1. наименьшее количество фигур на доске, и
2. наименьшее количество возможных ходов, и
3. ход белых, и
4. белым доступен всего один ход, без взятия фигуры противника, и
5. позиция должна быть реалистичной.

Поз. 9

Поз. 10

Поз. 11

Кстати, побить Каспарова могут не только гроссмейстеры

Шесть фигур, только пешки (поз. 9). — 3 (обсуждение) 18:14, 18 марта 2019 (UTC)

Или даже пять (см. поз. 10). José Monteiro _discussão 18:32, 18 марта 2019 (UTC)

О, здорово! А теперь убираем из поз. 10 черную пешку и получаем четыре фигуры (поз. 11). — 3 (обсуждение) 19:56, 18 марта 2019 (UTC)

Но ведь 1. ... Кр:c7. José Monteiro _discussão 20:02, 18 марта 2019 (UTC)

Позиции 10 и 11 нелегальные. У черных нет последнего хода. Позиция 9 - браво! Ясен Перец (обсуждение) 20:10, 18 марта 2019 (UTC)

Да, действительно. Поз. 10 не соостветствует условию 5, а в поз. 11 у черных есть лазейка. Не пойдет! Продолжаем искать вврманты -- можно ли обойтись четырьмя фигурами? — 3 (обсуждение) 20:21, 18 марта 2019 (UTC)

Или хотя бы пятью, коль действительно казус возник с поз. 10. José Monteiro _discussão 20:24, 18 марта 2019 (UTC) Кстати, позиция 10 легальна. Ей могли предшествовать ходы -1. с6 Крd8 0. с7+ Крc8. José Monteiro _discussão 20:28, 18 марта 2019 (UTC)

Точно, извиняюсь. Легальна, конечно. Эк меня торкнуло... Ясен Перец (обсуждение) 20:49, 18 марта 2019 (UTC)

Хозе меня опередил с комментарием.... Беру свои слова обратно по поз. 10. Она реальна. Положим черный король стоял на d8. Затем белые поставили шах пешкой на с7 и черные с дуру двинули короля на с8. Следующий ход белых -- пат. Так что всё норм. Следующая остановка -- пат четырьмя фигурами. — 3 (обсуждение) 20:41, 18 марта 2019 (UTC)

Даже не сдуру, а весьма предусмотрительно, иначе проигрывают с треском. А насчёт позиции с четырьмя фигурами — это уже сомнительно. José Monteiro _discussão 20:44, 18 марта 2019 (UTC)

Ой, и правда не сдуру, надо было заблокировать пешку. Про сомнительность четырех фигур я бы не загадывал, у нас есть еще Профессор, гениальный гроссмейстер, побивший Каспарова и IBM. Посмотрим, что он скажет. — 3 (обсуждение) 20:53, 18 марта 2019 (UTC)

Увы, я проверил все 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 475 возможных позиций (в уме, конечно) — при соблюдении всех условий (из которых второе лишнее) меньше, чем 5 фигурами, не обойтись. Тот Самый Профессор (обсуждение) 21:03, 18 марта 2019 (UTC)

Позиция 12. Белые ставят пат первым же ходом. Решение у этой задачки единственное. Ясен Перец (обсуждение) 13:46, 19 марта 2019 (UTC)

Конечно же, я решил. Я даже знаю, какой был последний ход чёрных. Тот Самый Профессор (обсуждение) 14:55, 19 марта 2019 (UTC)

Так мы все и поверили. José Monteiro _discussão 15:38, 19 марта 2019 (UTC)

Я хотел, чтоб и другие попробовали решить, но ты сам напросился: 0. … b7—b5 1. cb — пат. Тот Самый Профессор (обсуждение) 15:52, 19 марта 2019 (UTC)

В этой позиции интересно, что в ней все-таки есть одна лишняя фигура. При более детальном анализе выясняется, что, например, ладью на b8 вполне можно убрать, и решение все равно останется тем же самым. Или вместо ладьи можно убрать пешку е4. А вот убрать и ладью и пешку вместе уже нельзя - задача не будет иметь решения. Ясен Перец (обсуждение) 18:05, 19 марта 2019 (UTC)

Поз.12