Квадрат

Квадрат — четырёхугольник, у которого все углы прямые, все стороны равные, все диагонали перпендикулярные, да и вообще, всё что может быть равно у четырёхугольника, оно всё и равно.

Свойства

1. Основное отношение квадрата. Если в квадрате проведены обе диагонали, разбивающие квадрат на четыре прямоугольных треугольника, центры масс которых соединены между собой, то площадь образованного квадратика ровно в 4,5 раз меньше основного.
2. Теорема об окружностях и квадрате. Если в квадрат вписать окружность, и вокруг квадрата описать окружность, после чего квадрат незаметно вытащить, то получится две окружности, одна побольше, а другая поменьше.
3. Обобщённая теорема об окружностях и квадрате. Если в квадрат вписать окружность, в неё вписать квадрат, в новый квадрат вписать ещё одну окружность, а в новую окружность — новый квадрат, после чего незаметно вытащить все упоминавшиеся квадраты, то получится мишень.
4. Обобщённая обобщённая теорема об окружностях и квадрате. Если в квадрат что-нибудь вписать, а в это что-нибудь вписать ещё что-нибудь, и так продолжать пока не надоест, то после удаления квадрата получится что-нибудь, в которое вписано нечто, в которое вписано ещё что-то и так далее.
5. Теорема о разрезании квадрата. Если квадрат разрезать на две части, то сумма их площадей будет равняться площади квадрата.
6. Вторая теорема о разрезании квадрата. Любая прямая, проходящая через вершину квадрата и делящая одну из его сторон на две части, разбивает квадрат на фигуры, площади которых удовлетворяют соотношению Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle S_{1}=c*S_{2}} , где c — некоторое положительное число.

Признаки

По сути, те же свойства, но недостаточно интересные, чтобы их называли свойствами. Так, фигура является квадратом, если:

1. Максимально возможная длина стороны равностороннего треугольника, вписанного в фигуру, относится к стороне последней как Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\sqrt {6}}-{\sqrt {2}}} к $1$.
2. Длину фигуры легко спутать с шириной. В частности, квадратным является каждое второе одеяло.
3. При нахождении периметра и площади фигуры по формуле круга число $\pi$ равно 4.
4. У фигуры всего 4 вершины с равными расстояниями между каждыми двумя из них — а нет, это тетраэдр.
5. Слева и сверху от фигуры находятся буквы и числа соответственно, а внутри — точки и прямоугольники.
6. Под фигурой имеется подпись «Квадрат», подтверждённая авторитетными источниками.

Задачи о квадратах

Задачи для циркуля и линейки

Из самой древности пришли к нам задачи, которые имели какое-то отношение к квадрату и решались с помощью циркуля и линейки. Самыми известными такими задачами являются проблемы построения квадратов, по площади равных данным фигурам.

Квадратура квадрата

Наиболее примитивная из всех задач такого типа. Её суть заключалась в том, что имеется некоторый квадрат, циркуль, линейка и необходимость построить ещё один такой же квадрат. Задача решается достаточно просто.

Решение задачи о квадратуре квадрата  

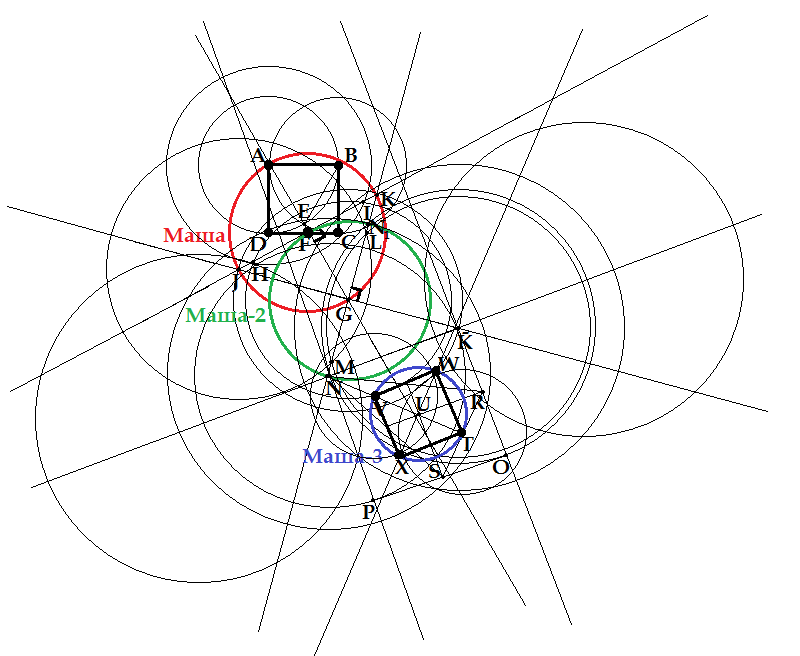
Пусть дан квадрат Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle ABCD} со стороной, равной 1.

Раствором циркуля, равным стороне квадрата, строятся две окружности с центрами в вершинах $A$ и $B$. Допустим, внутри квадрата они пересекаются в точке $E$. Затем через точку $E$ и вершину $A$ проводится прямая, которая пересекает сторону Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle CD} в точке $F$. Очевидно, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \bigtriangleup AEB} равносторонний, поэтому Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \angle EAB=60^{\circ }} , а Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \angle DAE=30^{\circ }} соответственно. Таким образом, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \bigtriangleup FDA} прямоугольный с острым углом Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \angle DAF=30^{\circ }} . Те, кто знают тригонометрию, скажут сразу, а те, кто тригонометрию не знают — немного подумав, что отрезок Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle DF={\frac {1}{\sqrt {3}}}} , а Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AF={\frac {2}{\sqrt {3}}}} .

Продлим прямую Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AF} куда подальше за точку $F$. Раствором циркуля, равным длине отрезка Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AF} построим окружность с центром в точке $F$. Там, где эта окружность пересекается с предусмотрительно продлённой прямой Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AF} с одной стороны внезапно оказывается точка $A$, а с другой — какая-то безымянная точка, которую мы окрестим точкой $G$. Эта окружность, которую мы провели, нам ещё пригодится, поэтому, для удобства, назовём её Машей.

Теперь построим две окружности равного радиуса, причём такого, чтобы он был явно меньше длины отрезка $AG$ и явно больше длины отрезка $AF$, с центрами в точках $A$ и $G$, которые, если радиусы выбраны правильно, должны пересечься в двух точках, которые нам назвать пока не довелось. Чтобы было интересней и веселей, назовём эти точки $H$ и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle I} .

Теперь мы можем построить прямую Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle HI} , которая мало того, что пересечёт прямую $AG$ в точке $F$, так ещё и под прямым углом. Продлим эту прямую до пересечения с окружностью, которую мы окрестили Машей, это даст нам ещё две хорошие точки, которые мы назовём $J$ и $K$.

Соединим точки $G$ и $J$, после чего внимательно посмотрим на Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \bigtriangleup GFJ} . Внутренний голос подсказывает, что это равнобедренный прямоугольный треугольник с катетами длиной ${\frac {2}{\sqrt {3}}}$. По теорема Пифагора можно посчитать, что та сторона, которая подлиннее, она же гипотенуза, она же основание, она же Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GJ} оказывается равна ${\sqrt {({\frac {2}{\sqrt {3}}})^{2}+({\frac {2}{\sqrt {3}}})^{2}}}={\frac {2{\sqrt {2}}}{\sqrt {3}}}$.

Итак, у нас есть отрезок Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GJ={\frac {2{\sqrt {2}}}{\sqrt {3}}}} . Чтобы было интереснее, продлим его куда-нибудь подальше, например, за точку $G$. Раствором циркуля равным длине отрезка Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GJ={\frac {2{\sqrt {2}}}{\sqrt {3}}}} построим окружность с центром в многострадальной точке $G$, которая, если пренебречь кривизной рук, мелкими погрешностями и неидеальностью Вселенной, пересечёт прямую Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GJ} в точке $J$ и ещё в одной, которую мы до сих пор не назвали. Срочно исправляем этот недостаток и называем её точкой Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}} (так как доказательство без использования букв с индексами, значками и умляутами — не доказательство, а детская забава).

Раз уже мы воткнули циркуль в точку $G$, не будем его оттуда доставать и проведём ещё одну окружность радиусом Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GF={\frac {2}{\sqrt {3}}}} . Это окружность также пересечёт прямую Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GJ} в двух точках, но мы их называть никак не будем, потому что они и не нужны вовсе. Некоторое время назад у нас была окружность по имени Маша. Забудьте про ту окружность. Отныне Машей называется эта окружность, с центром в точке $G$ и радиусом ${\frac {2}{\sqrt {3}}}$.

Далее построим две окружности равного радиуса, причём такого, чтобы он был явно меньше длины отрезка Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}J} и явно больше длины отрезка Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}G} , с центрами в точках Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}} и $J$, которые, по идее, должны пересечься в очередных двух неназванных точках, именуемых в дальнейшем $L$ и $M$.

Прямая Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle LM} , не имеющая к сигаретам никакого отношения, пересекает прямую Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}J} в точке $G$ и перпендикулярна ей. И это хорошо. Теперь эту прямую можно продлить в обе стороны до тех пор, пока она не пересечётся с окружностью Машей. Это породит очередные две точки, имя которым — Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle N} и $N_{1}$. Мы неспроста одну из точек назвали $N_{1}$ — дело в том, что она нам больше не понадобится, а английский алфавит и так грозит закончится на самом интересном месте решения. Зато точка Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle N} нам нужна, и очень. Мы её соединим с точкой Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}} , после чего тщательно посмотрим на Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \bigtriangleup NG{\bar {K}}} . После долго просмотра обнаруживаем, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle G{\bar {K}}=GJ={\frac {2{\sqrt {2}}}{\sqrt {3}}}} , а Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle GN=GF={\frac {2}{\sqrt {3}}}} .

И снова нам на помощь спешит Пифагор со своей бессмертной теоремой. Благодаря ей мы обнаруживаем, что: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}N={\sqrt {G{\bar {K}}^{2}+GN^{2}}}={\sqrt {({\frac {2{\sqrt {2}}}{\sqrt {3}}})^{2}+({\frac {2}{\sqrt {3}}})^{2}}}=2} . Ну ничего себе, не так ли?

Теперь надо быстренько построить квадрат со стороной Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}N} . Если вы внимательно читали это доказательство, то уже научились строить перпендикуляры к данной точке прямой. Поэтому будем считать, что вы смогли построить отрезки Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}O} и $NP$, равные по длине отрезку Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}N} и перпендикулярные ему.

Соединим точки $O$ и $P$. И что вы думаете? ${\bar {K}}NOP$ — квадрат, почти такой, как нам нужен, только в четыре раза больше.

Так вот, если вы внимательно читали решение задачи, то уже, наверное, научились находить середины отрезков. Так что опять будем считать, что вам не составило никакого труда найти середины отрезков Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}O} и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle OP} . Назовём эти точки точками $R$ и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle S} .

Построим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \bigtriangleup RNS} . Если вы дочитали доказательство до этого места, значит, в предыдущем абзаце вы смогли найти середины отрезков Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\bar {K}}O} и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle OP} , так что теперь вам не составит никакого труда найти середины всех трёх сторон этого треугольника и даже провести медианы. Самую длинную медиану, которая заодно высота и биссектриса, назовём медианой $NT$, а точку её пересечения с Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle RS}  — точкой $T$. Точку пересечения всех-всех медиан этого треугольника тоже как-нибудь назовём, например, точкой $U$.

Если вы всё построили правильно, то вы тут же заметите, что длина отрезка Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle TU} равна ровно-ровно Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\sqrt {2}}{2}}} . А это не что иное, как половина диагонали искомого квадрата.

Дальше остаётся только построить очередную окружность по имени Маша с центром в точке $U$ и радиусом Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {\sqrt {2}}{2}}} , получив таким образом точку $V$, построить перпендикуляр к прямой Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle TV} , пересекающий её в точке $U$, и обозначить точки пересечения этого перпендикуляра с окружностью Машей как точки Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W} и $X$.

Четырёхугольник Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle WTVX} и есть искомый квадрат. Заметим, что после решения задачи у нас остались не использованными буквы Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Z} и весь греческий алфавит, что характеризует это решение как достаточно краткое и рациональное.

Квадратура куба

Интересная задача, в которой даётся куб, циркуль и линейка; с помощью них нужно построить квадрат, равный данному кубу. Сложность задачи заключается в том, что до сих пор точно не установлено, как именно куб может быть равен квадрату. Существовали предположения, что квадрат равен кубу, если из него можно склеить такой куб. Однако такая оценка оказалась достаточно грубой, поскольку любой достаточно большой квадрат оказывался равен множеству маленьких кубиков. Тогда было введено уточнение, что квадрат равен кубу, если из этого квадрата можно склеить однослойный куб, причём весь квадрат окажется использован. Сразу же было обнаружено, что в этом случае задача достаточно легко разрешима, однако квадрат получается достаточно двенадцатиугольным. Окончательного решения задача до сих пор не имеет.

Кубатура квадрата

Задача, обратная задаче о квадратуре куба. Даётся квадрат, а с помощью циркуля и линейки необходимо построить куб. Интересным в данной задаче является то, что сам квадрат в ходе решения никак не используется — трудность составляет само по себе построение объёмного куба на плоской бумаге.

Задачи со спичками

В этих задачах используются, разумеется, не настоящие спички, которые могли бы в любой момент привести к пожару, а специальные деревянные палочки длиной 4 см с цветными утолщениями на конце, которые напоминают, очевидно, возбудителей дифтерии с зёрнами волютина только на одной стороне.

Построение 2 квадратов из 7 спичек

Требует незаурядных способностей и интеллекта, поскольку при обычном подходе к задаче всё время, как ни крути, не хватает одной спички. Лишь самые сообразительные смогут понять, в чём подвох, и решить задачу, укоротив все спички на 1/8 и сложив из 7 оставшихся маленьких кусочков недостающую сторону.

Построение 6 квадратов из 12 спичек и пластилина

На первый взгляд задача кажется сложнее, чем предыдущая, так как на каждый квадрат приходится уже не по 3,5, а по 2 спички. Но уже на второй взгляд в поле зрения попадает пластилин, и решение приходит само по себе: нужно просто построить 3 квадрата из спичек и слепить 3 квадрата из пластилина.

Интересные квадраты

• Произвольный квадрат со стороной 4 см. Редкий вид квадрата, иногда встречается в самых подлых и хитрых математических задачах. Его отличительной чертой является тот факт, что длины трёх его сторон и градусные меры его углов для нас покрыты завесой тайны и только в глубине души мы подозреваем, что этот квадрат не такой-то уж и произвольный.
• Магический квадрат. Волшебные свойства этого квадрата стали проявляться ещё в раннем детстве. Он умел читать мысли на расстоянии, гнуть поварёшки, засорять дырки в дуршлаге, менять цвет хамелеону и угадывать число.
• Дьявольский магический квадрат. Дьявольский магический квадрат представляет собой квадратную таблицу n*n, заполненную числами, причём по какому-то недоразумению сумма любых чисел этой таблице равна 666. Математически недостижим.
• Квадрат Паскаля. Четырёхугольный треугольник Паскаля, в котором в верхнем ряду все числа — единицы, а в каждом следующем каждое число равно сумме числа, стоящего в клеточке выше. Квадрат обладает уникальными свойствами: в частности, сумма любых n чисел из квадрата равна n.
• Мягкий квадрат. Фигура, которая внешне похожа на четырёхугольник; при этом все его стороны в большинстве случаев равны, а углы приблизительно по девяносто градусов каждый. Идеальный мягкий квадрат можно нарисовать с помощью карандаша с закрытыми глазами.

Квадраты в биологии

Перекрёстное деление квадрата в стадии анафазы II.

Научная классификация
Надцарство: Абстрактные Царство: Математические Тип: Геометрические Отдел: Планиметрические Класс: Многоугольники Отряд: Четырёхугольники Семейство: Параллелограммы Род: Прямоугольники Вид: Квадрат
Латинское название
Rectangulum Quadratum
[{{fullurl:wikispecies:{{{wikispecies}}}|uselang=ru}} Систематика на Викивидах] [{{fullurl:commons:Special:Search/{{{wikispecies}}}|uselang=ru}} Поиск изображений на Викискладе]

Некоторые биологи относят квадрат к роду Ромбы, что, конечно же, ошибочно. Любой школьник знает, что стороны ромба, в отличие от квадрата, проводятся не по горизонтали и по вертикали, а по диагонали. В зависимости от формата окружающей среды размер фигуры может варьировать от нескольких миллиметров до нескольких миль и даже больше, если начертить её на карте мира.

Ну и, собственно, самое интересное. Размножаются квадраты перекрёстным делением, при котором из материнского квадрата образуется 4 дочерних, а то и 16 внучатых или даже 64 правнучатых. В частности, самое молодое поколение квадрата-прапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрапрабабушки составляет 17592186044416 маленьких квадратиков.

Квадраты в культуре

Квадраты очень сильно повлияли на культуру человечества. Множество созданных картин имеют квадратную форму. Некоторые изображали квадраты на квадратных картинах, что символизирует, собственно, квадрат.

См. также

• Геометрия
• Абсурдотека:Квадратные стихотворения

Совет

Понравилось — покажи друзьям.