Геометрия
Геометрия — лженаучный раздел математики (полностью бесполезный), все объекты изучения которого преднамеренно упрощены до уровня сферического коня в вакууме. Однако, чтобы школьники (по крайней мере, отличники) не пускали самолётики и не бросались бумажками на уроке геометрии, как это делают на ОБЖ, эта наука была настолько усложнена учёными, что геометрический анализ упрощённых объектов стал гораздо сложнее, чем обычный анализ неупрощённых.
История[править]

Основоположником геометрии считается Евклид. Примерно 2300 лет назад он посетил Страну восходящего солнца, и, когда он проходил мимо одного из домов, ему на голову упал арбуз кубической формы, который, как оказалось, рос на грядке, находящейся на балконе. От такой тяжёлой ягоды Евклид получил сотрясение мозга, слишком сильное для того, чтобы открыть закон всемирного тяготения, и в результате он смог открыть лишь геометрию с её упрощёнными, как у упавшего арбуза, формами.
Применение геометрии в практических целях было известно ещё в Древней Греции. Известен случай, когда Архимеду понадобилось найти объём короны, имеющей, как известно, довольно сложную форму. Зная, что вычисление объёма путём погружения в воду даст серьёзную погрешность за счёт постепенного испарения и поверхностного натяжения, учёный решил прибегнуть к непосредственным измерениям, используя свои глубокие познания в геометрии. Установив, что форма короны наиболее близка к цилиндрической, Архимед измерил лишь высоту и диаметр короны и по формуле объёма цилиндра быстро вычислил искомый объём. В результате выяснилось, что бескорыстный ювелир не только израсходовал всё золото для изготовления короны, а ещё и добавил 10 кг от себя.
Основной проблемой геометрии в древние века, когда ещё не было таких графических редакторов, как Necrosoft Paint, было построение геометрических объектов с помощью циркуля и линейки. С помощью линейки учёные могли построить отрезок, ломаную линию и многоугольник, однако длина начерченных линий не могла превышать 30 см (точнее, с учётом всех делений линейки, 30,6 см). Ещё хуже обстояло дело с циркулем: этим инструментом можно было начертить только точку, которую оставлял грифель в центре, в то время как вращаемая вокруг него игла лишь царапала бумагу.
В настоящее время благодаря научно-техническому прогрессу учёные в состоянии выполнить любые геометрические построения, порой состоящие из десятков элементов, поэтому и основные проблемы геометрии стали гораздо более серьёзными.
Основные геометрические объекты[править]
Мельчайшей единицей геометрии является точка — объект нулевых размеров по всем параметрам, поэтому можно считать, что наличие точки тождественно её отсутствию, что подтверждается Малой теоремой Ферма. Эталоном точки в настоящее время считается душа кота Шрёдингера, которая аналогично существует и не существует одновременно. Фотон также предлагался в качестве эталона, но не был одобрен учёными по причине нефотоногеничности точки.
Изящное доказательство ничтожности размеров каждой отдельной точки продемонстрировал чемпион Праги по игре в точки Точек Ставица. За свою трёхмесячную профессиональную карьеру он сыграл 42 напряжённых матча, поставив в общей сложности более 3000 точек. Всё это время он использовал одну и ту же ручку. Более того, ею можно было писать даже после столь длительной эксплуатации, что свидетельствует о бесконечно малом объёме чернил, затрачиваемых на 1 точку, и, как следствие, её ничтожности.
Примером более крупного объекта может служить отрезок — часть прямой линии, которую отрезали от основной её части. Оставшуюся же обрезанную часть принято называть обрезком.
Сама по себе прямая линия, как и линия вообще — это геометрический объект, который под силу нарисовать обычному человеку. Если же прямая линия настолько длинная, что её может начертить разве что зацикленный аутист, то она не является линией по определению и именуется просто как прямая, длину которой условно принимают за бесконечность, чтобы не забивать голову большими числами.
Существует распространённое заблуждение, что если посмотреть прямой в торец, то можно увидеть точку. Ни в коем случае нельзя этого делать! Как только наблюдатель попытается заглянуть на прямую сбоку, прямая тут же проткнёт ему глазное яблоко и мозг и выйдет через затылок, устремившись в бесконечность. Но если всё-таки очень хочется взглянуть на прямую сбоку, то нужно предварительно разрезать прямую на 2 луча и только потом посмотреть на оба по очереди (смотреть только со стороны разреза!). Затем следует мысленно преобразовать обе увиденные точечные проекции в одну в соответствии с Малой теоремой Ферма (0=1; 1=2) и радоваться полученному результату, совпавшему с изначальным заблуждением.
Ещё более массивным по своей структуре объектом является плоскость — пространство, находящееся под постоянным давлением с обеих сторон, равным Па. Геометрические фигуры на плоскости — это не что иное, как бывшие объёмные тела, оказавшиеся под таким же давлением. Этот факт легко доказывается на практике на примере асфальтоукладчика и какого-либо объёмного человеческого тела, не обладающего высокой прочностью.
Величину всех основных геометрических объектов можно выразить в точках следующим образом:
- Точка — точка.
- Отрезок — точек.
- Луч — отрезков, или точек.
- Прямая — 2 луча, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2\infty ^{2}} точек
- Бесконечная полоса, ограниченная двумя параллельными прямыми — прямых, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2\infty ^{3}} точек.
- Полуплоскость — полос, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2\infty ^{4}} точек.
- Плоскость — 2 полуплоскости, или точек.
- Бесконечный слой, ограниченный двумя параллельными плоскостями — плоскостей, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 4\infty ^{5}} точек.
- Полупространство — слоёв, или точек.
- Пространство — 2 полупространства, или точек.
- Бесконечный объём, ограниченный двумя параллельными пространствами — пространств, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 8\infty ^{7}} точек.
- Полугиперпространство — объёмов или точек.
- Гиперпространство — 2 полугиперпространства или точек.
- Бесконечный гиперобъём, ограниченный двумя параллельными гиперпространствами — гиперпространств, или точек.
- Полугипергиперпространство — гиперобъёмов или точек.
- Гипергиперпространство — 2 полугипергиперпространства или точек.
- Апейрогиперпространство — 2 полуапейрогиперпространства или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \infty ^{\infty +1}} точек.
Для n-мерного геометрического объекта можно расчитать количество точек таким образом:
- Бесконечный Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-4)]} объём, ограниченный двумя параллельными Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-4)]} пространствами — Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-4)]} пространств, или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle (2^{n-1})\infty ^{(n*2-1)}} точек.
- ПолуНевозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-3)]} пространство — Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-4)]} объёмов или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle (2^{n-1})\infty ^{(n*2)}} точек.
- Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-3)]} пространство — полуНевозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle [giper*(n-3)]} пространства или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle (2^{n})\infty ^{(n*2)}} точек.
Параллельность и перпендикулярность прямых[править]
Теорема о непересекаемости параллельных прямых по праву считается одной из самых сложных в истории геометрии. Многие геометры, начиная с Евклида, пытались её доказать, но впервые это удалось сделать лишь в XIX в. Для этого понадобилось проложить рельсы, идентичные параллельным прямым, на протяжении, близком к бесконечному, в данном случае — от Москвы до Владивостока, после чего пустить поезд «Москва—Владивосток». Экспериментально было доказано, что, поскольку состав в течение всего пути ни разу не сошёл с рельс, то параллельные прямые действительно нигде не пересекаются. Однако, во избежание излишней громоздкости и больших материальных затрат, данная теорема вскоре была принята за аксиому.
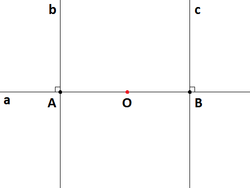
Менее сложной, но не менее интересной для геометров является теорема о трёх перпендикулярах, сформулированная следующим образом:
Дана прямая . Если существует прямая , перпендикулярная данной, то всегда можно построить ещё одну прямую , также перпендикулярную прямой .
Доказательство. Разделим прямую на 2 симметричных луча так, чтобы перпендикулярная ей прямая пересекала прямую слева от оси симметрии Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle O} . Так как симметричные части прямой абсолютно идентичны, то равноудалённые от оси Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle O} точка пересечения и точка справа также идентичны, чего нельзя сказать об остальных точках. Из этого следует, что точка также может быть местом пересечения двух перпендикулярных прямых ( и ), что и требовалось доказать.
Многоугольники[править]
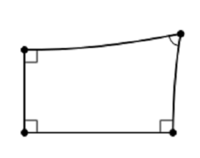
В глубокой древности люди умели считать только до 3, и все остальные числа, начиная с 4, они условно называли как «много». Именно поэтому первым начерченным многоугольником стал четырёхугольник. Все четырёхугольники можно подразделить на прямоугольники, имеющие прямые углы и прямосторонники, имеющие только прямые стороны. Ранее выделяли также кривосторонники, построенные лицами с малым радиусом кривизны рук и более низким расположением плечевого пояса, но, чтобы не портить такую изящную науку, как геометрия, кривосторонники были переименованы в определённые интегралы и удалены из геометрии, как инородные объекты.
Прямоугольники, в свою очередь, делятся на остропрямоугольники, имеющие помимо прямых хотя бы один острый угол, и тупопрямоугольники, в которых тупо все углы прямые. Среди них выделяют трапецию — прямоугольник, у которого одна сторона расположена дальше от наблюдателя, чем противоположная. Если же прямоугольник настолько длинный, что дальняя его сторона скрывается за горизонтом, то такой частный случай трапеции называется треугольником.
Круг — общее название для нольугольника и правильного бесконечноугольника (нифигона и дофигона соответственно), которые не имеют видимых различий, но всё же отличаются между собой. Если нольугольник — это просто гипертрофированная точка, то правильный бесконечноугольник — это полноценный многоугольник, каждая крайняя точка которого является одновременно и стороной, и вершиной так называемого наноразвёрнутого угла, невидимого невооружённым глазом.
Теорема Пифагора[править]
Простейшая геометрическая теорема, которую под силу доказать даже первокласснику. Дело в том, что множество доказательств теоремы бесконечно, поэтому любая попытка обосновать её приводит к неизбежному успеху. Ниже представлены самые распространённые доказательства теоремы Пифагора:
- Арифметико-физический метод исключения. Заметим, что гипотенуза имеет ту же размерность, что и катеты. То же самое можно сказать и про их квадраты, поэтому квадрат гипотенузы не может быть произведением или частным квадратов катетов. Теперь заметим то, что мы не заметили в прошлый раз: гипотенуза больше, чем любой из катетов, и это неравенство сохраняется при возведении их всех в квадрат. Значит, квадрат гипотенузы также не может быть разностью квадратов катетов. Методом исключения мы устанавливаем, что квадрат гипотенузы может быть равен только сумме квадратов катетов, что и требовалось доказать.
- Университетский метод исключения. Задаём студенту-двоечнику, пришедшему на последнюю переэкзаменовку, доказать теорему Пифагора. Одно из двух: либо он её доказывает, либо мы исключаем его из университета.
- Метод школьника. Да на лоха отвечаю, что равен!
- Метод лоха. Рассмотрим . У него есть 3 стороны: , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AC} и . Также у него есть 3 вершины: точка , точка и точка . Ещё у него есть 3 угла: , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \angle B} и . Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \angle C=90^{\circ }} , величина двух других углов неизвестна, но нам это и не требуется. Угол, равный 90°, называется прямым, то есть — это прямой угол. Треугольник, имеющий прямой угол, называется прямоугольным, то есть — это прямоугольный треугольник. Сторона противоположна , значит, — это гипотенуза . Стороны Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AC} и не противоположны , следовательно, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle AC} и — катеты . Сторона короче, чем , поэтому — это короткий катет , а — длинный катет . Теперь рассмотрим более подробно…
- Метод Деда Мороза. В этом году гипотенуза вела себя в 2 раза лучше, чем катеты, поэтому ей мы подарим большой квадрат, а менее послушным катетам — по квадрату с вдвое меньшей площадью. В итоге квадрат гипотенузы по площади оказался равен сумме квадратов катетов, и так будет до тех пор, пока катеты не исправятся.
- Доказательство от противного. Предположим, что квадрат гипотенузы не равен сумме квадратов катетов. Но тогда бы никакой теоремы Пифагора не было. Возникает противоречие, следовательно, наше предположение ошибочно. Теорема доказана.
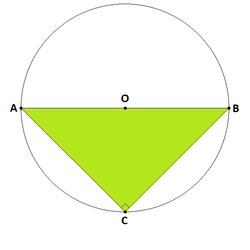
Однако, несмотря ни на что, единственным канонически верным с точки зрения геометрии является следующее доказательство:
Проведём описанную окружность вокруг прямоугольного . Её центр находится на середине гипотенузы, которая также является диаметром этой окружности и делит на 2 равные части. Следовательно, дуга, стягиваемая гипотенузой равна сумме двух дуг, стягиваемых катетами и . Пропорциональность между дугами, стягиваемыми катетами и гипотенузой, и квадратами последних наукой пока не доказана, поэтому она принимается за аксиому. Теорема доказана.
В простонародии эта теорема получила название «Пифагоровы трусы» за сходство её графического представления с трусами (вид сзади), которые носил сам Пифагор, а также нижней частью спины и выглядывающими из-под трусов ногами древнегреческого учёного.
Примеры простейших задач в планиметрии[править]
Нахождение периметра треугольника[править]
Дано: — равносторонний
- = = = 10 см[1]
Найти: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{ABC}}
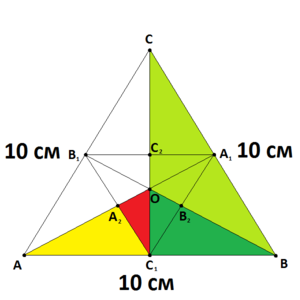
Решение. Очевидно, что вычислить периметр невозможно без дополнительных построений. Чтобы не мелочиться и не прибегать по ходу решения к каким-либо ещё построениям, проведём сразу 3 биссектрисы, 3 медианы, 3 высоты (которые почему-то совпадают на чертеже) и 3 средние линии. Получившийся красивый узор свидетельствует о том, что мы на верном пути.
Рассмотрим . Он прямоугольный с допустимой небольшой погрешностью. С такой же погрешностью предполагаем, что и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \angle A_{2}C_{1}O=30^{\circ }} , с целью более лёгкого и рационального решения. Сторона Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle A_{2}C_{1}} составляет половину средней линии и равна Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2,5} см, см. По теореме Пифагора Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle OC_{1}={\sqrt {(2,5)^{2}+({\frac {2,5{\sqrt {3}}}{3}})^{2}}}={\frac {5{\sqrt {3}}}{3}}} см. Отсюда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{A_2OC_1} = 2,5 + \frac{7,5\sqrt3}{3}} см.
Теперь рассмотрим Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup AA_2C_1} . Его углы также равны Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 30^\circ} , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 60^\circ} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 90^\circ} в порядке возрастания, значит, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup AA_2C_1} подобен Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup A_2OC_1} . Короткий катет рассматриваемого треугольника совпадает с длинным катетом предыдущего, что значительно облегчает вычисление Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{AA_2C_1}} . Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AA_2 = A_2C_1 * ctg30^\circ = 2,5\sqrt3} см. Заметим, что гипотенуза предыдущего треугольника оказалась ровно в 2 раза длиннее, чем короткий катет, поэтому и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AC_1 = 2 A_2C_1 = 5} см. Следовательно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{AA_2C_1} = 7,5 + 2,5\sqrt3} см.
Рассчитаем коэффициент подобия Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup A_2OC_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup AA_2C_1} через их периметры для большей надёжности, поскольку погрешность суммы 3 сторон значительно меньше, чем каждой по отдельности:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{7,5 + 2,5\sqrt3}{2,5 + \frac{7,5\sqrt3}{3}} = \frac{3 + \sqrt3}{1 + \frac{3\sqrt3}{3}} = \frac{3 + \sqrt3}{1 + \sqrt3} * \frac{1 - \sqrt3}{1 - \sqrt3} = \frac{3 - 2\sqrt3 - 3}{1 - 3} = \sqrt3}
Рассмотрим Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup OBC_1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup CBC_1} . Полное и развёрнутое решение предусматривает также рассмотрение ещё 30 треугольников, но мы этого делать не будем, чтобы решить эту задачу в кратчайшие сроки. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup CBC_1} также подобен Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup OBC_1} , и короткий катет первого треугольника также совпадает с длинным катетом второго. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{OBC_1} = \frac{5\sqrt3}{3} + 5 + \frac{10\sqrt3}{3} = 5 + 5\sqrt3} см.
Благодаря найденному коэффициенту подобия, справедливому и для этих треугольников, нам не нужно суммировать длины сторон Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup CBC_1} , чтобы узнать периметр. Достаточно Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{OBC_1}} умножить на коэффициент: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (5 + 5\sqrt3) * \sqrt3 = 15 + 5\sqrt3} см.
Рассмотрим условие задачи. Стороны Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \bigtriangleup ABC} — рациональные числа, поэтому иррациональная часть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P_{CBC_1}} — это не что иное, как проведённая высота Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle CC_1} . Избавляемся от неё и умножаем полученную разность на 2: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 15 * 2 = 30} см. Получившееся рациональное, целое и даже круглое число свидетельствует о том, что задача решена правильно.
Ответ: 30 см.
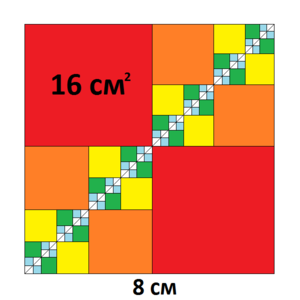
Нахождение площади квадрата[править]
Дано: Безымянный[2] квадрат со стороной 8 см Найти: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle S}
Решение. Разделим данный квадрат по диагонали на 2 равные части и впишем в каждую из них по квадрату (на рисунке обозначены красным цветом), со стороной, вдвое меньшей, чем у искомого квадрата, то есть 4 см. Как известно, квадрат со стороной 4 см — это частный случай многоугольника, когда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P=S=16} (см² для площади). Аналогичным образом вписываем в оставшуюся область 4 квадрата поменьше (жёлтого цвета), затем 8 квадратов ещё меньше (зелёного цвета) и т. д. Заметим, что площадь каждого из вписываемых квадратов каждый раз уменьшается в 4 раза, а их количество увеличивается в 2 раза. Найдём предел образовавшейся последовательности, приняв площадь квадрата со стороной 4 см за единицу:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \lim_{n \to \infty} x_n = 2*1 + 4*\frac{1}{4} + 8*\frac{1}{16} + \cdots + 2^n*\frac{1}{2^{2n-2}} = 2+1+\frac{1}{2}+\cdots+\frac{1}{2^{n-2}} = 4}
Как видим, безымянность данного квадрата отрицательно сказалась на индивидуализации подхода к нему и привело к куда более краткому решению по сравнению с другими многоугольниками, обозначенными буквами. Поэтому правильный ответ Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 16*4 = 64} см² нельзя считать достоверным без ряда дополнительных проверок.
Ответ: 64±32 см².
Объёмные тела[править]
Простейшим объёмным телом в геометрии считается пирамида — произвольный многоугольник со смещённым центром тяжести, не совпадающим с плоскостью этого многоугольника. Причина этого воистину удивительного феномена неизвестна, но большинство геометров полагает, что она кроется в тех же магнитных аномалиях, что и в случае с пересекающимися параллельными прямыми. Как результат, диагонали такого многоугольника, проходя через центр, становятся рёбрами пирамиды, а проведённый серединный перпендикуляр — апофемой.
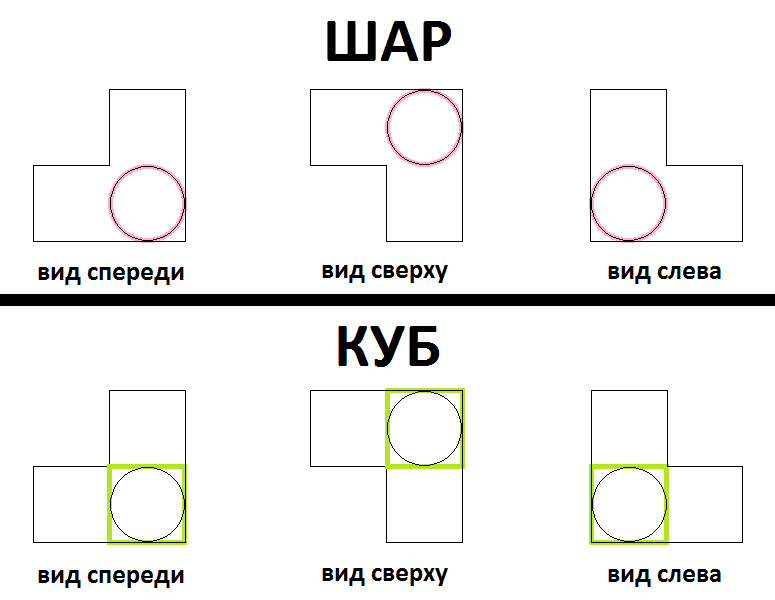
Цилиндр — вспомогательное тело, самостоятельная значимость которого не показана. Используется исключительно для графического представления таких объёмных тел, как шар и куб.
Дело в том, что форма двух вышеперечисленных тел настолько сложна, что они не подвластны человеческому воображению. Простейший способ получения шара и куба заключается в следующем. Берут 3 равных цилиндра и «сваривают» их таким образом, чтобы «свариваемые концы» цилиндров равнялись диаметру их оснований, и чтобы каждый из этих тел был перпендикулярен двум другим. Полученная область, принадлежащая всем трём цилиндрам, называется шаром, а область, принадлежащая хотя бы двум из них — кубом.
Кроме того, к объёмным телам однажды хотели отнести тор, на что великий учёный Э. Торричелли, быстро сообразив, что это — типичный объект топологии (см. ниже), лаконично высказался: «Тор здесь неуместен». Впоследствии эта фраза стала крылатой: позже её использовали не только в математике, но и в других областях науки, лишь слегка изменив её, чтобы не нарушать авторское право.
«Неуместные» цитаты[править]
Топология[править]
Топология (дословно верхняя наука от англ. top — верх и греч. λόγος — наука), также высшая геометрия — углублённый раздел геометрии, основанный крайне увлечёнными своей деятельностью математиками, пожертвовавшими ради науки своей личной жизнью. Этим объясняется тот факт, что объектами изучения топологии являются любые фигуры или тела, имеющие дырки. Порой учёные-топологи настолько озабочены этими отверстиями, что не могут отличить даже кружку от бублика только потому, что у них обоих есть по одной дырке.
Лента Мёбиуса[править]
Величайшее изобретение немецкого тополога А. Мёбиуса, получившего патент на него ещё в юности. В то время, как его ровесники клеили девушек, Мёбиус, будучи прирождённым топологом, клеил бумагу. Однажды, в процессе очередного эксперимента с бумагой, учёный решил рискнуть и повернул вырезанную полосу перед склейкой на 180°. Ещё никто из топологов не осмеливался пойти на это до него: такая инверсия в их кругу считалась перверсией и насилием над бумагой.
Мёбиус неоднократно подвергался критике за своё «безнравственное» изобретение, поэтому тополог решил собрать побольше народу и продемонстрировать свойства этой замечательной полоски. На глазах у публики он полностью разрезал ленту вдоль, и — о чудо! — она не распалась на 2 части, а стала в 2 раза длиннее и у́же! Полученную полоску Мёбиус опять разрезал вдоль. При этом она всё-таки распалась на 2 части, но они удивительным образом оказались соединены между собой.
Но зрители, будучи неглупыми людьми, быстро догадались, что это развод, и Мёбиус специально посещал курсы иллюзиониста, чтобы их одурачить. Так, в первый раз, по мнению публики, тополог незаметно спрятал 2 части своей ленты в рукав и одновременно вытащил спрятанную заранее длинную и узкую ленту; во второй раз он незаметно отклеил одну из 2 полосок, прикрывая место разъединения пальцем, и приклеил обратно.
Чтобы доказать, что это не фокус, а научный факт, Мёбиус обратился к «Разрушителям легенд». Естественно, ему со смехом было отказано, поскольку в эксперименте с «какой-то бумажкой» было бы нецелесообразно что-либо взрывать. Отчаявшись, Мёбиус решил покинуть топологию и стал фокусником, заработав впоследствии немало денег благодаря «фокусу» с одноимённой лентой.
Бутылка Клейна[править]
Объект топологии, в 2 раза более интересный, чем лента Мёбиуса, так как имеет 2 дырки: вход в бутылку и сквозную дырку снаружи её. Это — единственная бутылка, внутри которой невозможно собрать корабль. Многие топологи пытались это сделать, используя изогнутые по плоскости зажимы и пинцеты, но конфигурация горлышка не позволяла совершать внутри бутылки Клейна точные и скоординированные манипуляции. В конце концов «прогрессивные геометры» плюнули на эту затею, заявив от безысходности, что у этой чёртовой бутылки нет «снаружи» и нет «внутри».
Геометрия Лобачевского[править]
В детстве Лобачевский был чрезвычайно ранимым мальчиком и сильно обижался, когда ему говорили, например, что дважды два равняется не пяти, как он думал, а четырём. Однажды в школе на вопрос учителя он уверенно заявил, что через точку, не лежащую на прямой, можно провести не менее 20—30 прямых, параллельных ей. Получив двойку, Лобачевский поклялся, что создаст свою геометрию, в которой все до единой прямые, а также другие линии, будут параллельными друг другу.
Едва окончив университет, амбициозный геометр воплотил свою идею в реальность. В геометрии Лобачевского ни одна из линий не только не пересекается с другой, а даже не примыкает к ней. В соответствии с принятым постулатом многоугольники в геометрии Лобачевского не имеют вершин, а их изолированные друг от друга стороны устремляются в бесконечность. Благодаря этому задачи на вычисление периметра и площади становятся неактуальными: обе эти характеристики численно равны бесконечности[3].
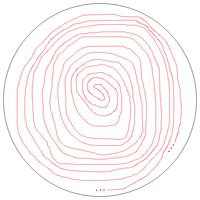
Особый интерес представляет прямая, заключённая внутри окружности (границы нольугольника) — единственного замкнутого объекта в геометрии Лобачевского. Поскольку прямая аутопараллельна (не может пересекать саму себя) и параллельна окружности согласно постулату, то ей ничего не остаётся делать, как скрутиться в бесконечную спираль.
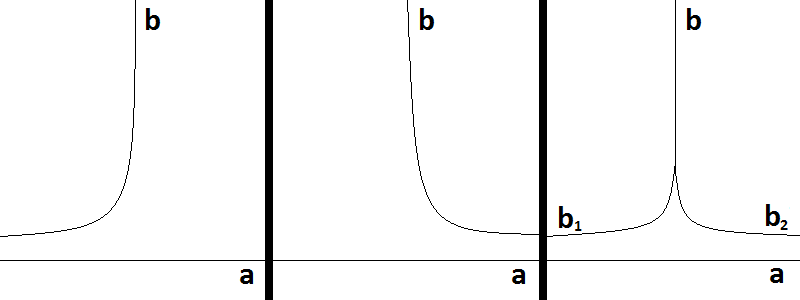
Геометрия Лобачевского получила практическое применение и в других разделах математики, в частности, в математическом анализе. Например, в так называемых координатах Лобачевского область значений и область определения функции никогда не включает в себя 0, чтобы график не смог пересечь оси абсцисс и ординат, а точка (0; 0) выколота из координат вообще, причём выколота не «кружочком», а иголкой, чтобы оси ни в коем случае не пересекались.
Однако геометрия Лобачевского не лишена недостатков. До сих пор остаётся загадкой, как поведёт себя прямая, которая в евклидовой геометрии была бы перпендикулярна другой. Ведь с равной вероятностью она может повернуть как влево, так и вправо, или же вообще раздвоиться и пойти в обе стороны.
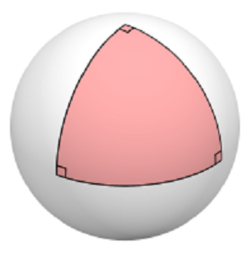
Сферическая геометрия[править]
Сферическая, или глобальная, геометрия — относительно современный раздел геометрии, в котором плоскостью служит планета Земля. Остальные, более древние, разделы были основаны ещё в те времена, когда Землю ошибочно считали плоской. После появления глобальной геометрии все они были объединены под общим названием локальная геометрия, в которой кривизной планеты можно было пренебречь.
С появлением принципиально нового раздела многоугольники стали дифференцировать на выпуклые (в глобальной геометрии) и невыпуклые (в локальной геометрии). Поскольку выпуклые многоугольники изогнуты красиво и равномерно, то они кривосторонниками не считаются, поэтому их существование в геометрии вполне допустимо.
В Новое время, по аналогии со сферической геометрией, сформировался целый класс так называемых телоидных геометрий: пирамидальная, коническая, призматическая, цилиндрическая, кубическая и т. д. Последняя ввиду общего «трицилиндрического» представления стала самой популярной из них.
Кубическая геометрия[править]
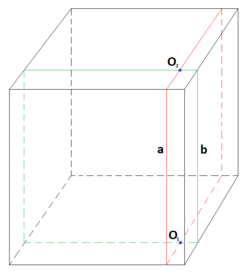
Основой данной геометрии является замкнутая гексаплоскость, изогнутая под прямым углом в 12 местах. Её главный постулат звучит так:
Каждый из объектов кубической геометрии, за исключением точки, должен располагаться не менее, чем на 2 гранях сразу, иначе он будет неотличим от такового в евклидовой геометрии, что недопустимо и неинтересно.
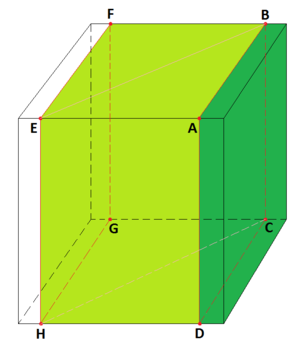
Из приведённого постулата следует, что все вершины многоугольников должны лежать на рёбрах куба, поскольку угол — это также геометрический объект, и образующие его стороны должны находиться на соседних гранях. Сами стороны при этом самостоятельными объектами не считаются.
В треугольнике, как в таковом, все стороны являются соседними по отношению друг к другу; то же самое можно сказать и о гранях, на которых они лежат. Следовательно, вершина, в которой сходятся эти грани, лежит внутри данного треугольника и представляет собой смещённый центр его тяжести. Иными словами, треугольник в кубической геометрии — это, по сути, пирамида.
Куда больший интерес, чем треугольник, вызывает квадрат, обладающий уникальными свойствами:
- Каждый угол квадрата равен 180°, образованный суммой двух прямых углов с ребром куба.
- Сторона квадрата и, как следствие, периметр равны константе.
- Площадь квадрата может находиться в пределах Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a^2 < S < 5a^2} , то же касается и прямоугольников (как, например, прямоугольник Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle EBCH} на рисунке).
Примечательно, что круг, описанный по «экватору» куба, визуально неотличим от квадрата. Это послужило графическим решением задачи о квадратуре круга.
Примеры практического применения геометрии[править]
- На стрельбище, где несколько человек стреляют по мишеням, траектории полёта пуль проходят по практически параллельным прямым. Зная аксиому о непересекаемости параллельных прямых, стрелки́ могут не бояться, что какая-нибудь шальная пуля отскочит от другой и попадёт в одного из них. У тех ж стрелков, кто не знаком с этой аксиомой, настолько дрожат руки от страха травмоопасного рикошета, что они могут выстрелить с отклонением до 30°, что может привести с травмоопасному рикошету из-за пересечения уже совсем непараллельных траекторий.
- Жарким летом часто возникает желание спрятаться от палящих солнечных лучей в своём доме, однако даже тут коварное солнце ярко светит через окно! Для человека, знающего геометрию, это не беда: представив освещаемый объём комнаты в виде призмы с трапецией в основании (длинное основание трапеции — путь лучей от верхнего края окна до пола, короткое основание — от подоконника до пола) и измерив угол падения солнечных лучей, он легко сможет вычислить, где не нужно находиться, чтобы избежать прямых солнечных лучей. Людям же, не знающим геометрии, приходится в этой ситуации использовать плотные шторы или жалюзи.
- Некоторые ради экстремальных ощущений любят прыгать с парашютом, рискуя жизнью (или без него, рискуя жизнью ещё больше). Теперь допустим, что парашют не раскрылся. Тогда, при отсутствии сильного ветра, будущая жертва будет падать по прямой, перпендикулярной земной поверхности. Рассмотрим точку пересечения прямой и «земной» плоскости. Именно здесь в ближайшую минуту и будет лежать разбившийся парашютист. Если учесть, что через произвольную точку в пространстве можно провести только одну прямую, перпендикулярную плоскости, то можно сделать вывод: знающий это парашютист может не знать, где он упадёт, чтобы подстелить солому в нужном месте — ему достаточно знать, откуда он выпрыгнет.
- Применение в медицине. При имплантации груди необходимо (и достаточно) знать всего лишь координаты центра шара, через который мысленно производим сечение плоскостью Лобачевского модели Пуанкаре. На выходе имеем две полусферы. Распространённая ошибка решения: полусферы получаются неравными. P.S. Клей Момент должен быть в НУ (начальные условия).
Примечания[править]
- ↑ В геометрии горизонт, за которым скрывается вершина треугольника, может находиться на любом расстоянии от наблюдателя.
- ↑ Когда этому квадрату попытались дать название, появилось сообщение «Фигура с именем „ABCD“ уже существует. Введите другое имя».
- ↑ Расстояние между соседними сторонами по мере удаления в бесконечность не стремится к нулю. Начиная примерно со 100 км от центра многоугольника, его стороны полностью распрямляются и перестают приближаться друг к другу. Отсюда следует, что площадь такого многоугольника не имеет предела.
См. также[править]

|
Медаль лучшей статьи По итогам голосования от 24 февраля 2012 статья Геометрия была признана лучшей статьёй четвёртого полуторагодия после исторических шахмат и форума о мыле, наравне с философией. В соответствии с волеизъявлением народных масс ей выдаётся эта медаль. Поздравляем! |