Как правильно:Обнаружить перпендикулярные и параллельные миры
| Библиотека дельных советов |
| Как правильно |
|---|
⚒ |
| Кладезь мудрости |
| Вводная часть · Все руководства · Случайное руководство |
| Найти дельный совет |
| Определения терминов |
Сейчас Вы приобщитесь к великой тайне вселенной, и научитесь определять положение в пространстве мест, параллельных и перпендикулярных тем, где Вы так плодотворно познаёте науки.
Для этого Вам не придётся прорывать усилием воли пространственно-временной континуум. Не придется совмещать инвариантность реальностей. Для этого не нужно резать мозгом пространство. Не нужно прогрызать червоточины сквозь космос. Вам вообще не придётся покидать вашу родную планету, ибо эти миры находятся прямо на ней.
Всё, что Вам понадобится — это географическая карта мира. И некоторые знания из геометрии, арифметики и географии.
Определение условностей[править]
Чтобы никого не обидеть, предположим, что все мы в данный момент времени жители города Урюпинска, и всем нам захотелось попутешествовать в миры, параллельные и перпендикулярные нашему чудесному городу.
Мы принимаем основание земной коры, на которой так уютно расположился Урюпинск, за плоскость.
«Это не корректно!!!» — возразят самые умные из Вас, Земля имеет форму геоида, или, если уж в приближении к Евклидовой геометрии — сфероида. А значит, основание города — часть некой выпуклой сферообразной поверхности. И Вы будете правы. НО простейшие расчеты доказывают, что этой кривизной мы смело можем пренебречь.
Итак: мы имеем исходные данные. Аппроксимированный радиус земного сфероида — 6371000 м. Наибольшая протяжённость между границами городского периметра примерно 5670 м.
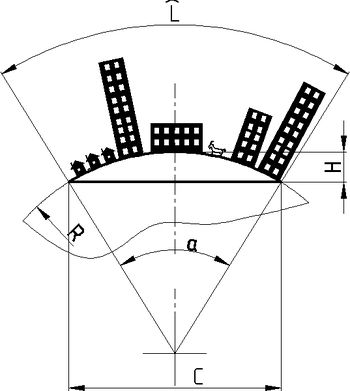
Из геометрии нам хорошо известна формула высоты кругового сегмента (рис.1): Н = с/2 х tg(α /4), где Н — высота хорды сегмента, с-длина хорды этого сегмента, α-угол, между стягивающими сегмент радиусами.
Длина хорды легко вычисляется по формуле: с = 2R х sin(α/2), где R — радиус сегмента. Подставив значение с из второй формулы в первую получим: Н = 2R/2 х sin(α/2) х tg(α /4), помня о том, что tg(α /4) = sin(α/4)/cos(α/4) и sin(2α) = 2sin(α) х cos(α) и сократив коэффициенту при R, получим - Н = R х 2sin(α/4) х cos(α/4) х sin (α/4)/cos(α/4), сокращаем подобные и получаем в итоге - Н = R х 2sin ²(α/4).
Угол вычисляется по формуле α = 57,296L/R, где L — длина дуги сегмента, в нашем случае — расстояние между границами городского периметра.
Таким образом: α = 57,296 х 5670/6371000; α = 0,051º
Окончательно подставив числа в формулу, получим: Н = 6371000 х 2sin ²(0,051º /4) = 0,631 м, что составляет примерно 0,000099 % от величины радиуса Земли. То есть в процентном отношении — ничтожную величину. Ею мы смело пренебрегаем.
Поиск перпендикулярных миров[править]
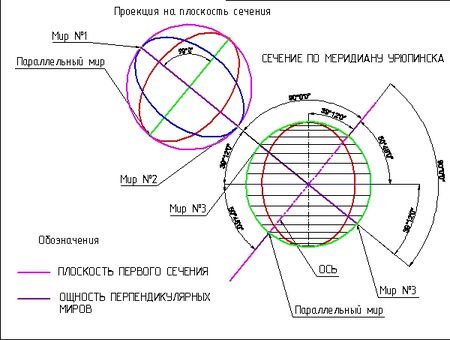
Усвоив множество мемуаров путешественников — великих, средних, а также ниже среднего, мы можем прийти к выводу: каждая страна, каждый регион на Земле — это свой собственный, неповторимый, самобытный мир. Как вы понимаете, на Земле их множество. Начнём же поиск перпендикулярных миров, поскольку наш Урюпинск, как и всякий географический объект, имеет свои общепринятые географические координаты. А именно: 50º 48’ СШ; 42º01’ВД (рис.2).
- Мысленно представим себе ось, проходящую через геометрический центр основания Урюпинска и центр земного шара. Все уже догадались, что эта ось перпендикулярна основанию Урюпинска. Обозначим её ОСЬ. Теперь проведём плоскость, ориентированную с запада на восток содержащую ОСЬ.
Мы определили, в какой плоскости будем определять наши первые перпендикулярные миры.
- В данном случае для определения мы будем оперировать долготой.
Для примера начнём вращать плоскость основания Урюпинска относительно центра Земли против часовой стрелки.
- Этот мир будет расположен на экваторе. (см.рис.3)
Долгота вычисляется простейшим арифметическим действием.
- Нам необходимо изменить долготу на 90º в сторону уменьшения, поскольку мы договорились первый мир определять против хода часовой стрелки.
- 42º01’ мы поворачиваем до гринвичского меридиана, сразу за которым начинается западная долгота.
Нам необходимо ещё «довернуть» ещё на 47º59’ЗД.
- Координаты первого перпендикулярного мира: 0 Ш; 47º59’ЗД.
- Так-с, посмотрим на карту… Это координаты прибрежной части Бразилии в устье Амазонки. Это водный мир, так что если будете его посещать — не забудьте акваланг, ласты, подводную лодку и тротил, на случай встречи с пираньями.
Не любите плавать, или вовсе не умеете? Не беда, ибо этот перпендикулярный мир — не единственный.
- Повернём теперь в этой же плоскости сечения по часовой стрелке.
Для упрощения опускаем вычисления. Координаты: 0 Ш; 132º01’ ВД. — это Индонезийский остров Вайгео, один из Зондских островов.
Райское местечко — курорт. Сказочный экзотический мир. Казалось бы, можно остановится здесь, но — нет! Пытливый научный ум должен быть выше плотских удовольствий, так что…
- …продолжим поиски. Теперь развернём плоскость сечения около выбранной ранее ОСИ. Для удобства повернём новую плоскость на 90º к первой.
- Сразу становится ясным — теперь мы оперируем в меридиональной плоскости.
- Снова мысленно повернём плоскость основания Урюпинска на 90º против часовой стрелки.
Пройдя оставшиеся 39º12’, мы окажемся на северном полюсе, минуем его и перейдём в западное полушарие на 137º59’ ЗД.
- Таким образом, третий перпендикулярный мир имеет координаты 39º12’СШ;137º59’ ЗД. И к нему диаметрально расположен перпендикулярный мир № 4: 39º12’ЮШ 42º01’ВД.
Куда же это мы попали? Вот: перпендикулярный мир № 3 — Тихий океан, зато прямо на пересечении Морских торговых путей, можно намыть остров и брать плату за проход.
Перпендикулярный мир № 4 — снова океан, но уже Индийский, глухое место, малопосещаемое, если нужно побыть одному, собраться мыслями, помедитировать, лучше места не найти.
Но и это ещё не всё. Поскольку до сих пор мы оперировали только в двух плоскостях. А таких плоскостей, проведённых по оси, проходящей через центр Земли и перпендикулярно основанию Урюпинска — бесконечное множество. Все они образуют общность перпендикулярных миров, описывая замкнутую кривую по поверхности земли — след перпендикулярных миров.
Определяемся с параллельным миром[править]
Теперь определимся с параллельным миром. Проблема в том, что свойство транзитивности, успешно применяемое в двух измерениях в трёхмерном пространстве, здесь не действует. Например, мир № 1 перпендикулярен Урюпинску, мир № 3 также перпендикулярен, в двух измерениях мир № 1 и мир № 3 были бы параллельными, но в трёх измерениях они между собой снова перпендикулярны.
Так что, для определения параллельного мира вернёмся к нашим выбранным ранее секущим плоскостям. Помня о том, что угол между параллельными плоскостями равен 0º или 180º, мы просто в обеих плоскостях мысленно повернём наши полученные перпендикулярные миры дальше на 90º, против часовой стрелки.
Что же мы видим: плоскости совпали, и как бы мы ни прокладывали другие секущие плоскости через ОСЬ, поворот на 180º приведёт нас всегда на одно и то же место. То есть в пределах нашей планеты, каждому месту, в нашем случае Урюпинску соответствует только один параллельный мир. Его координаты: 50º 48’ ЮШ; 137º59’ ЗД. Снова Тихий океан. Снова глушь.
Но если есть желание и GPS-навигатор, можно побывать и там.
Конечно же, вселенная не ограничивается нашей планетой, и где-то там, хрен знает где, существуют ещё параллельные и перпендикулярные миры. Но чтобы посетить их Вам придётся прорывать усилием воли пространственно-временной континуум, совмещать инвариантность реальностей, резать мозгом пространство, прогрызать червоточины сквозь космос и заниматься прочей хренью, что так любят делать британские учёные. А оно Вам надо?