Кривая Криворукова

Загогулина, понимаешь…

~ Ельцин про кривую Криворукова

Генератор кривой Криворукова

Упрощенная версия генератора кривой Криворукова

Кривая Криворукова — кривая, каждая точка которой расположена в точке с координатой A(a, b), причём обязательно выполняется одно из двух условий: либо a=b, либо нет. Впервые была получена Криворуковым в его прописях, впрочем, он пытался выдать кривую за предложение «Мама мыла раму». В итоге уже с первого класса у Криворукого было два по чистописанию и Нобелевская премия по математике.

Определение

Первое определение кривой Криворукова дал сам Криворуков. Оно звучало именно так:

Кривая Криворукова — связное компактное топологическое пространство C топологической размерности 1, располагающееся в баннаховом множестве третьего порядка.

Впрочем, придя в себя, Криворуков перечитал своё определение, понял в нем только слово «третьего» и переделал его. Новое определение звучало так:

Кривая Криворукова — кривая, которая, по-видимому, обладает какими-то свойствами.

Уравнения

Кривая Криворукова задаётся уравнением

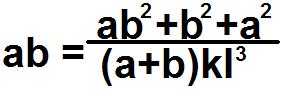
Где a, b, k, l — какие-то переменные, которые задаются, как попало, и не факт, что имеют какое-то отношение к кривой.

Свойства

Криворуков, получив кривую, вывел эту формулу. Правда, так и не понял, что она означает и зачем он это вообще вывел

• Если на координатной плоскости точка с наименьшим значением функции расположена в точке (х, у) то точка с наибольшим значением функции может быть где угодно. Предположительно значение функции точки с наибольшим значением функции не меньше, чем значение функции точки с наименьшим значением функции.
• Кривая Криворукова пересекает ось Ox во всех точках вида (N, 0), причём N является каким-то числом, а 0 принадлежит промежутку (-259, 325).
• Длина некоторых кривых Криворукова выражается эллиптическим интегралом 2-го рода, некоторых — эллиптическим интегралом 3-го рода, а некоторых — вообще не выражается и ведёт приличный образ жизни.
• Чтобы нарисовать кривую Криворукова, надо начертить какую угодно линию и снизу подписать «кривая Криворукова 11-го рода». Впрочем, можно написать, что эта кривая какого угодно рода, потому что все равно никто деления на роды кривых Криворукова не совершал. На этом основании можно полагать, что уравнение кривой Криворукова: $y=f(x);x=g(y)$.
• Частными случаями кривой Криворукова являются олимпийские кольца, карты метро, планы эвакуации и решётка для крестиков-ноликов.
  

  Частный случай кривой Криворукова. Получается, если параметр принять за 461 и придумать, куда его всунуть
• В принципе, кривую Криворукова можно изобразить и в трёхмерном пространстве. В таком случае, уравнение имеет вид: $x=f(y;z);y=g(z;x);z=h(x;y).$
• Для четырёхмерного пространства: $x=f(y;z;t);y=g(z;t;x);z=h(t;x;y);t=i(x;y;z).$
• А для пятимерного: $x=f(y;z;t;u);y=g(z;t;u;x);z=h(t;u;x;y);t=i(u;x;y;z);u=j(x;y;z;t).$