0=1

Художественный метод доказательства

Малая теорема Ферма (ноль равняется единице; число ноль равняется числу один) — основной постулат всеобщего равенства, на основании которого доказывается равенство любых двух чисел (например, для доказательства $a=b$ обе части равенства умножаются на $a-b$, после чего к ним прибавляется $b$). Доказательство малой теоремы Ферма, а следом за ней и Самой последней теоремы Ферма о всеобщем равенстве, стало настоящим прорывом в математике, благодаря которому были пересмотрены многие гипотезы и теории в самых различных науках. В частности, был обобщён второй постулат Эйнштейна специальной теории относительности: благодаря теоремам Ферма было показано, что скорость любого тела, да хоть бы и не тела, не зависит от скорости движения источника и одинакова во всех инерциальных системах отсчёта.

Малая теорема Ферма доказывается многими — похожими и отличающимися — методами.

Математические методы

Арифметические методы

Метод умножения

Вариант 1.

Справедливо равенство $0\cdot 0=0\cdot 1$. Поделим это выражение на $0$. Получим:

${\frac {0}{0}}\cdot 0={\frac {0}{0}}\cdot 1\,$

отсюда выходит, что $0=1$.

Вариант 2. Упрощённый.

Дано: $0\cdot 0=0\cdot 1$. Так как $0=0$, то $0=1$, тем же можно доказать всеобщее равенство всех чисел нулю.

Метод преобразования дробей

Вариант 1. Вынесение общего множителя у дробей.

Справедливо равенство

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {4}{4}}={\frac {5}{5}}}

Вынесем общий множитель:

$4\cdot {\frac {1}{1}}=5\cdot {\frac {1}{1}}$

Сократим: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 4=5} . Вычтем 4 и получим искомое равенство.

Вариант 2. Преобразование равенства.

Допустим, что есть некое равенство $a-b=0$. А теперь поделим каждую сторону это равенства на $a-b$. Получим:

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {a-b}{a-b}}={\frac {0}{a-b}}\,}

или Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1=0} .

Вариант 3. Деление на ноль.

Справедливо выражение

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {a}{a}}=1\,}

значит

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {0}{0}}=1\,}

но

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {0}{0}}=x} ($x$ — любое число).

Возможно, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle x=0} , в таком случае, $0=1$.

Метод двоичной арифметики

В двоичной арифметике число $0$ можно изобразить или как $0:0$, или как Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1:0} . Однако, это по-прежнему одно и то же число. Сравнивая значения знаковых битов, следует вывод, что они могут быть только равны: $0=1$.

Обобщённый арифметический метод

Было бы гораздо удобнее считать, если бы 0 было равно 1, ведь тогда все числа равны друг другу и все выражения равны. Поэтому вводим новую аксиому: 0 = 1. Доказано.

Алгебраические методы

Метод степеней нуля

Вариант 1. Возведение в степень.

Следует обратить внимание, что

(1) Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a^{0}=1\,}

однако

(2) Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0^{a}=0}

Подставим $a=0$. Следовательно формуле (2), Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0^{0}=0} , но, исходя из формулы (1), Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0^{0}=1} . Таким образом, $0=1$, что и требовалось доказать.

Вариант 2. Степени единицы.

Как известно, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1^{a}=1} , таким образом, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1^{1}=1^{0}=1} . Но, если равны основания степеней и их значения, то равны и показатели, то есть $0=1$, что и требовалось доказать.

Метод логарифмирования

Согласно формулам, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \log _{a}a=1} и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \log _{a}1=0} . Подставим Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a=1} . Получим: из первой формулы Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \log _{1}1=1} , но из второй формулы Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle \log _{1}1=0} . Это значит, что $0=1$, что требовалось доказать.

Алгебраический метод

Метод, подобный предложенному в статье «Всеобщее равенство». Рассмотрим равенство

$a=b+c$

Умножим обе его части на $a-b$. Получим:

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a^{2}-ab=ab+ac-b^{2}-bc\,}

то есть

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a^{2}-ab-ac=ab-b^{2}-bc}

Разложим на множители, получим

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a(a-b-c)=b(a-b-c)\,}

сокращаем, получаем $a=b$. То есть, подставив Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a=1} , $b=0$, получим требуемое равенство. Впрочем, этот метод годится для доказательства равенства всех чисел.

Метод составления уравнения

Возьмём $x=1$. Это то же самое, что и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle x-1=0} . Добавим $x$, получим: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2x-1=x} . Вычитаем единицу: $2x-2=x-1$. Выносим общий множитель за скобку: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2(x-1)=x-1} , и полученное выражение делим на Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle x-1} . Получаем: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 2=1} . Вычитая из этого равенства единицу, получаем искомое выражение: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1=0} . Что и следовало доказать.

Метод сравнения

Возьмем два произвольных положительных равных числа $a$ и $b$ и напишем для них следующие очевидные нестрогие неравенства: Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a\geq -b} , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle b\geq -b} . Перемножив оба эти неравенства почленно, получим неравенство Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle ab\geq b^{2}} , а после его деления на $b$, что вполне законно, так как по условию Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle b>0} , придём к выводу, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a\geq b}

Записав же два других столь же бесспорных неравенства Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a\geq -a} , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle b\geq -a} . Действуя аналогично предыдущему получим, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle ab\geq a^{2}} , а разделив на $a$ (так как Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a>0} ), придём к неравенству $b\geq a$.

Итак, Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a\geq b\geq a} , что возможно только при $a=b$. Если Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle a=4} , Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle b=5} , то получим, что Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 4=5} , откуда, отняв от обеих частей равенства $4$, получим $0=1$.

Рис. 1. Равные треугольники

Метод констант

Два неоспоримых равенства:

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 0=const}

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1=const}

А если равны правые части выражений, значит равны и левые. Следовательно:

$0=1$

Геометрические методы

Метод треугольника

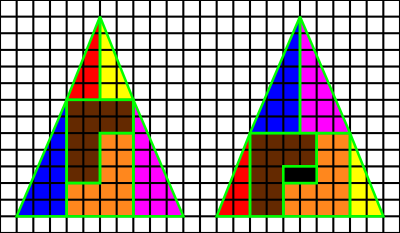
Вариант 1 (по рис. 1).

Рассмотрим два треугольника, представленных на рисунке. Площадь первого треугольника равна Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 60} клеточкам, а площадь второго треугольника, составленного из тех же фигур, что и первый треугольник, равна Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 58} клеточкам (две чёрные клетки внутри вырезаны). Получается, что

$58=60$

Отнимем от обеих частей равенства Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 58} и разделим на $2$, получим

Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle {\frac {58-58}{2}}={\frac {60-58}{2}}\,}

то есть $0=1$, что и требовалось доказать.

Рис. 2. Чертёж

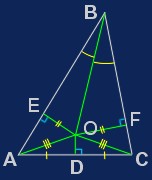
Вариант 2 (по рис. 2).

Докажем сначала, что все треугольники — равносторонние. Рассмотрим произвольный $\Delta ABC$. Проведем биссектрису угла $B$ и серединный перпендикуляр к стороне $AC$; точку их пересечения назовём $O$. Опустим из неё перпендикуляры Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle EO} и Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle OF} на стороны $AB$ и $BC$ соответственно.

Так как Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle DO} одновременно и высота, и медиана $\Delta AOC$, то он равнобедренный и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AO=OC} . Так как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BO}  — биссектриса, то, из равенства Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta EBO} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta OBF} (откуда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle EB=BF} ), Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle EO=OF} . Следовательно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta AEO=\Delta FCO} , то есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AE=FC} . Отсюда, так как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB=AE+EB} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BC=BF+FC} , Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB=BC} . Проведя такое же рассуждение для основания не Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AC} , а, например, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB} , получим, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle BC=CA} .

Из этого следует, что все треугольники на свете — равносторонние.

Теперь рассмотрим прямоугольный Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \Delta ABC} с гипотенузой Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB} . По доказанному выше, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB=BC=AC=a} , а по теореме Пифагора, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle AB^2=BC^2+AC^2} . Имеем: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a^2=2a^2} или Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=2} . Отнимем от обеих частей равенства Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} , получим Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать.

Неправильный нольугольник

Правильный нольугольник

Метод нольугольника

То, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , можно убедится, рассмотрев геометрическую фигуру нольугольник, у которой одна сторона и ноль углов. Учитывая, что в любом многоугольнике каждая сторона ограничена двумя вершинами, то есть углами, и из любого угла выходят две стороны, получаем, что число углов должно быть равно число сторон. То есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Тригонометрический метод

Вариант 1

Исходное утверждение	Следовательно	Отсюда	А значит
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sin0=\sin\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\pi=1\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}\,0=\mathrm{tg}\,\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\pi=1\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{cosec}\,0=\mathrm{cosec}\,\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\pi=1\pi}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать

Вариант 2

Исходное утверждение	Следовательно	Отсюда	А значит
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos\frac{\pi}{2}=\cos\frac{3\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\pi}{2}=\frac{3\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3=2}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sec\frac{\pi}{2}=\sec\frac{3\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\pi}{2}=\frac{3\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3=2}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{ctg}\,\frac{\pi}{2}=\mathrm{ctg}\,\frac{3\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\pi}{2}=\frac{3\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3=2}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать

Вариант 3 (сокращённый)

Исходное утверждение	Следовательно	А значит
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sin\frac{\pi}{4}=\cos\frac{\pi}{4}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sin0=\cos0}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sin\frac{\pi}{4}=\cos\frac{\pi}{4}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sin\frac{\pi}{2}=\cos\frac{\pi}{2}}	Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать

Комплексное исчисление

Иррациональный метод

Докажем сначала, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=-1} . Понятно, что ${\sqrt {-1}}={\sqrt {-1}}$. Представим части равенства так:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -1=\frac{-1}{1}}

и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -1=\frac{1}{-1}}

Получим

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt {\frac{-1}{1}}=\sqrt {\frac{1}{-1}}}

Известно, что корень из дроби есть корень из числителя делённый на корень из знаменателя. Поэтому

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\sqrt{-1}}{\sqrt1}=\frac{\sqrt1}{\sqrt{-1}}}

По свойству пропорции

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt{-1}\cdot\sqrt{-1}=\sqrt1\cdot\sqrt1}

Следовательно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -1=1} . Прибавив к обеим частям равенства Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} и разделив их на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} , получим требуемое равенство Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Канадский метод

Вариант 1. Основной.

Метод, предложенный канадскими учёными. Понятно, что

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{-1}{1}=\frac{1}{-1}}

Значит,

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt {\frac{-1}{1}} = \sqrt {\frac{1}{-1}}}

Таким образом,

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\sqrt {-1}}{\sqrt1}=\frac{\sqrt1}{\sqrt {-1}}}

Так как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt {-1}=i} , запишем равенство следующим образом:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{i}{1}=\frac{1}{i}}

Разделим обе части на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} , получим

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{i}{2}=\frac{1}{2i}}

Далее, прибавим к обеим частям равенства выражение Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{3}{2i}} , получим

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{i}{2}+\frac{3}{2i}=\frac{1}{2i}+\frac{3}{2i}} .

Теперь умножим обе части на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i} , получим

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i(\frac{i}{2}+\frac{3}{2i})=i(\frac{1}{2i}+\frac{3}{2i})}

раскроем скобки:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{i^2}{2}+\frac{3i}{2i}=\frac{i}{2i}+\frac{3i}{2i}}

Так как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i^2=-1} , получаем

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{-1}{2}+\frac{3}{2}=\frac{1}{2}+\frac{3}{2}} .

Посчитав, получим, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=2} , а отняв Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} , найдём требуемое равенство: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Вариант 2. Упрощённый.

Возьмём равенство из предыдущего варианта:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{i}{1}=\frac{1}{i}}

По правилу пропорций,

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i\cdot i=1\cdot1}

то есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -1=1} . Из последнего вытекает, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=2} . Делим на 2 и получаем искомое равенство Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Метод комплексных логарифмов

Используя формулу Эйлера, вычисляем:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{\pi i} = \cos(\pi) + i \sin(\pi) = -1 + 0i = -1 \,}

и

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{3\pi i} = \cos(3\pi) + i \sin(3\pi) = -1 + 0i = -1 \,}

поэтому

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{\pi i} = e^{3\pi i}}

Берём логарифм

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \ln(e^{\pi i}) = \ln(e^{3\pi i}) \,}

И получаем

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \pi i = {3\pi i} \,}

Делим обе части на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \pi i} :

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1 = 3}

Отсюда:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0 = 1}

Метод комплексных степеней №1

Используя формулу Эйлера, вычисляем:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{\pi i} = \cos(\pi) + i \sin(\pi) = -1 + 0i = -1 \,} , в полярной системе e^πi = (1, -π)

Но по определению степени комплексного числа в полярной системе

(r, θ)^x = (r^x, θx)

то есть

e^πi = (e, 0)^πi = (e^πi, 0).

Значит,

(1, -π) = (e^πi, 0),

то есть

-π = 0

Прибавим π:

0 = π

Поделим на π:

0 = 1, что и требовалось доказать.

Метод комплексных степеней №2

Согласно всё той же формуле Эйлера, имеем:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{\pi i} = -1}

Так как в правой части равенства стоит действительное число, то и число в левой части также действительное. Значит, можно возвести обе части равенства в квадрат:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e^{2\pi i} = 1}

Поскольку 1 - это е в нулевой степени, следовательно Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2\pi i = 0} , а значит Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i = 0} .

Возводя обе части этого равенства в четвертую степень, получаем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1 = 0} , что и требовалось доказать.

Векторно-комплексный метод

Известно, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i = \sqrt{-1} } . Вычислим квадрат этого равенства:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i^2 = -1 }

С другой стороны, в стандартной прямоугольной декартовой системы координат используется вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec i = (1,0,0) } , задающий направление вдоль оси X. Также найдём его квадрат:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec i^2 = (1,0,0)\cdot(1,0,0) = 1 }

Заметим, что указывать значок вектора ("стрелочку") над квадратом вектора не обязательно, т.к. это число. Получаем:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec i^2 \equiv i^2 = 1 }

Однако, мы уже знаем, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle i^2 = -1 } . Значит, верно, что:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1 = - 1 }

Прибавив к обеим частям равенства Невозможно разобрать выражение (Ошибка преобразования. Сервер («https://en.wikipedia.org/api/rest_») сообщил: «Cannot get mml. Server problem.»): {\displaystyle 1} и разделив их на Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} , получим требуемое равенство Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Стоит отметить, что этот метод универсальный, т.к. он работает и для мнимой единицы, обозначаемой через Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle j } (такое обозначение используется в электротехнике). Просто заметим, что в декартовой системы координат есть и вектор Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec j = (0,1,0) } , задающий направление вдоль оси Y. Его квадрат также равен единице, так что все приведённые вычисления оказываются верны и в этом случае.

Математический анализ

Метод производных

Вариант 1.

Как известно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x'=1} при любом Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} . Но, подставив вместо Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} любое число, получаем, что производная становится равной Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} . Следственно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Вариант 2.

Известно, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1'=0} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0'=0} . То есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0'=1'} , отсюда следует, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Метод интегрирования

Проинтегрируем функцию Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle f(x)=\frac{1}{x}} :

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \int f(x)dx=\int \frac{dx}{x}=\frac{1}{x}\cdot x - \int \frac{-1}{x^2}\cdot x dx=1+\int \frac{dx}{x}} .

Итак, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Метод бесконечных рядов

Рассмотрим сумму бесконечного ряда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle S=1+1-1+1-1+1-1...} . Представим его в виде

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle S=1+(1-1)+(1-1)+(1-1)...=1+0+0+0...=1} .

Теперь представим S теми же слагаемыми, но начиная с последнего. Имеем

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle S=-1+1-1+1-1+1-1...=-1+(1-1)+(1-1)+(1-1)...=-1+0+0+0...=-1}

то есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle S=1=-1} , значит Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=-1} , откуда, как указывалось выше, вытекает, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=0} .

К подобному выводу также приводит рассмотрение ряда Гранди.

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0 = \sum_{n=1}^\infty 0 = \sum_{n=1}^\infty (1-1) = 1 + \sum_{n=1}^\infty (-1 + 1) = 1\,}

Сокрад наблюдает за убегающей единицей

Метод убегающей единицы

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{align}1&=1+0+0+0+0+0+\cdots\\ &=0+1+0+0+0+0+\cdots\\ &=0+0+1+0+0+0+\cdots\\ &=0+0+0+1+0+0+\cdots\\ &=0+0+0+0+1+0+\cdots\\ &=0+0+0+0+0+1+\cdots\\ &\vdots\\ &=0+0+0+0+0+0+\cdots\\ &=0\end{align}}

Метод Крамера

Рассмотрим систему линейных уравнений

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left\{ \begin{matrix} c_1x_1 + c_1x_2 + \cdots + c_1x_n = c_1\\ c_2x_1 + c_2x_2 + \cdots + c_2x_n = c_2\\ \vdots \\ c_nx_1 + c_nx_2 + \cdots + c_nx_n = c_n \end{matrix}\right. }

Разделив первое уравнение на c₁, получим: x₁ + x₂ + · · + x_n = 1. Теперь решим систему методом Крамера.

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{bmatrix} c_1 & c_1 & c_1 & \dots\\ c_2 & c_2 & c_2 & \dots\\ \vdots&\vdots&\vdots&\\ c_n & c_n & c_n & \dots \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{bmatrix} = \begin{bmatrix} c_1\\ c_2\\ \vdots\\ c_n \end{bmatrix}}

Поскольку каждый столбец матрицы коэффицентов равен вектору свободных членов:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A_i = A \implies |A_i| = |A| \implies {|A_i| \over |A|} = 1 = x_i} для всех i.

Подставляя в уравнение x₁ + x₂ + · · · + x_n = 1, мы получаем:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sum_{i=1}^n 1 = 1} .

То есть:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle n=1}

Теория чисел

Факториальный метод

Обычно факториалы разных чисел имеют разное значение. Однако Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0!=1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1!=1} , то есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0!=1!} . Ссылаясь на ранее написанное, можно сказать, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Обобщённые цепные дроби

Мы знаем, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=\frac{2}{3-1}} . Заменим 1 в знаменателе на правую часть данного неравенства и повторим так бесконечное число раз: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=\frac{2}{3-\frac{2}{3-\frac {2}{3-...}}}}

Но проделывая тоже самое с равенством Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=\frac{2}{3-2}} , получаем, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=\frac{2}{3-\frac {2}{3-\frac{2}{3-...}}}} .

Полученные цепные дроби равны, следовательно Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=2} . Вычитая из обоих частей Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} , получаем, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Quod erat demonstrandum.

Метод смены системы счисления

Возьмем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 02} , поменяем систему счисления на двоичную, получим Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 10} . Значит Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 02=10} и в частности Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=0} .
Проверка: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Умножаем на 2.
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=2} . От смены приравниваемых истинность не меняется, поэтому:
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=0} . Получили второй результат.
Доказано с двойной точностью.

Математическая логика

Метод булевой алгебры

По общепринятой версии, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1^0=1} , но в булевой алгебре Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1^0=0} . Очевидно, что $0=1$.

Софизм

Известно, что если половина одного числа равна половине другого числа, то эти числа равны. Но полупустое ведро — это то же самое, что полуполное. Следовательно, пустое ведро равно полному. Значит, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

0 ничего (слева) = 1 ничего (справа)

Индуктивный метод

0 ничего = 1 ничего.
0 копеек = 1 копейка.
0 баллов = «кол» = 1 балл
0 микробов = 1 микроб.

Так как эти частные случаи выполняются, значит, по индукции получаем:
0 чего угодно = 1 чего угодно.
или
Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Адедуктивный метод

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Умножим обе части на 0. Получим Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=0} , что очевидно верно. Как известно из основ логики, если из нашего утверждения следует верное утверждение, значит оно верно. Доказано.

Обобщённо-математический метод

В математике все постулируется. Значит, весь вопрос в том, что постулировать — Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\ne1} или Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Выбираем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Доказано.

Физические методы

Метод крупных величин

Рассмотрим выражение Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 10^{100} = 10^{100}} . Так как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 10^{100}} значительно больше 1, то единицей всегда можно пренебречь. Следовательно, прибавив 1, мы существенно ничего не изменим. Получаем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 10^{100} = 10^{100}+1} . Отнимем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 10^{100}} , получим требуемое Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0 = 1} .

Метод ядерного взрыва

Вариант 1. Аккуратно соединим два (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} ) куска плутония докритической массы. Счастливо избежав гибели, останемся с пустыми руками (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} ). Таким образом, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2 = 0} . Разделив обе части уравнения на два получаем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=0} , или Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1}

Вариант 2. Запустим ядрёную бомбу с помощью межгалактичмежконтинентальной ракеты (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} ). С большой вероятностью она будет сбита системой ПВО (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} ). В результате удачи не останется ничего (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} ). Если же ракета-перехватчик промажет, то ядрёная бомба взорвётся по ударе о землю и останется одна ракета перехватчик (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} ).

Таким образом, либо Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=0} , либо Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=1} . Разделив на два первое утверждение и отняв единицу от обоих частей второго получаем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=0} , или же Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1}

Транспортно-железнодорожный экспериментальный метод, вариант 1

Проведите следующий физический эксперимент, когда будете идти по платформе со стороны хвоста поезда и увидите, например, стоящий на путях восьмивагонный состав. Сообщите другу: «встречаемся у третьего вагона с хвоста». При этом друг, идущий со стороны головы поезда, дойдя до этого вагона отсчитает шесть полных вагонов: ведь третий с хвоста вагон в восьмивагонном составе будет шестым с головы. Но так как всего вагонов восемь, то:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 8=6+3} , сложим 6 и 3:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 8=9} , и наконец после сокращения на 8 получим искомое:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Транспортно-железнодорожный экспериментальный метод, вариант 2

Как известно, подвижной состав российских и финских железных дорог полностью совместим, не смотря на то, что колея железной дороги различается: в Финляндии 1524 мм, а в России — 1520 мм. Следовательно, это одна и та же ширина колеи, то есть

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1524=1520}

Вычтем справа и слева 1520, а затем разделим правую и левую часть на 4:

Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=0} .

Астрономический метод

Рассмотрим вселенную до и после большого взрыва. Опишем состояние до как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} , после — как Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} . Так как, очевидно, вселенная не изменилась, то получаем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0 = 1}

Метод программирования

Общепрограммерский метод

Первый элемент массива часто обозначается нулевым индексом. Значит, первый — это нулевой. Отсюда выходит, что один равно нулю, а ноль одному: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Пример программы:

#include <stdio.h>

void main()
{
  int* a = new int[10]; //массив
  int n = 1; //номер элемента массива
  int i = 0; //счётчик

  for(; i < 10; i++) //пробегая весь массив
  {
    a[i] = n; //присваиваем текущему элементу его номер
    n++; //увеличиваем номер
  }

  printf("Элемент массива с номером 0 (a[0]) имеет номер %d", a[0]);
  //Выведет:
  //Элемент массива с номером 0 (a[0]) имеет номер 1
  //Следовательно, 0 = 1
}

Метод С++

См. код: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a=0;} Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a=a+1;} . Подставляя Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} , получаем, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать.

Примечание: этот факт не является точным, так как строка Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a==a+1} , то есть «Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} точно равно Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a+1} », выдаёт «false», то есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} не точно равно Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a+1} .

Упрощённый метод С++

Возьмём строку из предыдущего метода: Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a=a+1;} . Вычтем Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} , и получим искомое равенство Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Метод Malbolge

Если написать Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} в коде на языке Malbolge, а за ним Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} , то они после расшифровки будут одной и той же командой, то есть Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} делают одно и то же, или Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} .

Метод очевидного

Очевидно, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Доказано.

Юридический метод

Пока ещё никто не доказал, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\ne1} . Значит, необходимо считать, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1}

Общенаучные методы

Вики-метод (оформительный)

В любом вики-проекте 3 тильды дают только подпись, 5 тильд — только время, а 4 — подпись и время. Отсюда Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3+5=4} ; Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 8=4} . Разделим обе части на 4 (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=1} ) и вычтем по единице (Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1=0} ). По свойству коммутативности Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать.

Метод для ленивых

Если верить материалам статьи «Всеобщее равенство (математика)», все числа равны между собой и равны Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0} , значит, и Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} в частности.

Метод для умных ленивых

Исходя из определения всеобщего равенства, берём числовое равенство Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2=\sqrt{2}} . Как известно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -log_{2}log_{2}2=0} , а Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -log_{2}log_{2}\sqrt{2}=1} , следственно, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} , что и требовалось доказать.

Антинаучные методы

Метод от противного

Предположим, что Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1}  — это неверное равенство.
Ну и зачем мы это все столько времени доказывали? Незачем. Противно.
Значит, быть этого не может.
Но факт или есть, или нет. Пришли к противоречию.
Итак, Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1}  — верное равенство.

Очевидно неправильный

Так же называется методом добавления утверждения.

Рассмотрим два утверждения:
1. Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1}
2. Оба утверждения ложны.

Предположим, что второе утверждение истинно. Тогда первое и второе ложно. Пришли к противоречию. Значит второе ложно и хотя бы одно утверждение из двух истинно.
Мы уже доказали, что второе не может быть истинным, значит истинно первое — Невозможно разобрать выражение (MathML с запасными SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0=1} . Что и требовалось доказать.

Очевидно неправильный 2

Берём пример из прошлого примера:
1. 0=1
2. Оба утверждения ложны.
Если второе утверждение истинно - оно же ложно. Предположим, что второе утверждение верно. Второе утверждение утверждает, что оно неверно, то есть 0 (неверно) = 1 (верно).

Художественный метод

См. иллюстрацию в заголовке статьи.

Вики-метод

Вики-метод/1

{{#ifexpr: 0=1|true|false}} → true — что и требовалось доказать.

Вики-метод/2

{{#expr: 0}} → 1 — что и требовалось доказать. {{#expr: 1}} → 0 — что и требовалось доказать.

Вики-метод/3

{{#ifexpr: 1^0=1^1|true|false}} → true — что и требовалось доказать.

Лингвистический метод

Английский

В английском языке есть выражение «in no time» = «в мгновение ока».

Примем 1 мгновение ока за единицу.

Тогда:

• «in no time» = «в мгновение ока» | дословный перевод
• в никакое время = в 1 единицу времени | убираем время
• 0=1

Что и требовалось доказать.

См. также

• Всеобщее равенство
• Список чисел

Совет

Понравилось — покажи друзьям.